
【题目】如图,已知多面体![]() 是正方体,
是正方体,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上的动点,过点
上的动点,过点![]() ,
,![]() ,
,![]() 的平面与棱
的平面与棱![]() 交于点
交于点![]() ,则以下说法不正确的是( )
,则以下说法不正确的是( )
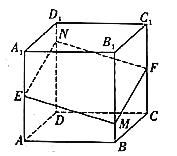
A.四边形![]() 是平行四边形
是平行四边形
B.四边形![]() 是菱形
是菱形
C.当点![]() 从点
从点![]() 往点
往点![]() 运动时,四边形
运动时,四边形![]() 的面积先增大后减小
的面积先增大后减小
D.当点![]() 从点
从点![]() 往点
往点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积一直增大
的体积一直增大
【答案】C
【解析】
对选项逐一判断,可得答案.![]() 项,由面面平行的性质定理可得
项,由面面平行的性质定理可得![]() ,故四边形
,故四边形![]() 是平行四边形.
是平行四边形.![]() 项,由
项,由![]() 是正方体,易知
是正方体,易知![]() 平面
平面![]() ,
,![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() ,故平行四边形
,故平行四边形![]() 是菱形.
是菱形.![]() 项,菱形
项,菱形![]() 的面积
的面积![]() ,线段
,线段![]() 的长度是定值,菱形
的长度是定值,菱形![]() 的面积先减小后增大.
的面积先减小后增大.![]() 项,由
项,由![]() ,点
,点![]() 到平面
到平面![]() 的距离不变,当点
的距离不变,当点![]() 从点
从点![]() 往点
往点![]() 运动时,三角形
运动时,三角形![]() 的面积一直增大,故三棱锥
的面积一直增大,故三棱锥![]() 的体积一直增大.
的体积一直增大.
如图所示
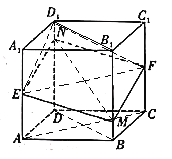
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() ,同理
,同理![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,故
是平行四边形,故![]() 正确.
正确.
![]() 是正方体,
是正方体,![]() ,又
,又![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() .
.
![]() 分别是棱
分别是棱![]() 的中点,
的中点,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,![]() 平行四边形
平行四边形![]() 是菱形,故
是菱形,故![]() 正确.
正确.
菱形![]() 的面积
的面积![]() ,线段
,线段![]() 的长度是定值.当点
的长度是定值.当点![]() 从点
从点![]() 往点
往点![]() 运动时,线段
运动时,线段![]() 的长度先减小后增大,
的长度先减小后增大,![]() 菱形
菱形![]() 的面积先减小后增大,故
的面积先减小后增大,故![]() 不正确.
不正确.
![]() ,点
,点![]() 到平面
到平面![]() 的距离不变.当点
的距离不变.当点![]() 从点
从点![]() 往点
往点![]() 运动时,三角形
运动时,三角形![]() 的面积一直增大,
的面积一直增大,![]() 三棱锥
三棱锥![]() 的体积一直增大,故
的体积一直增大,故![]() 正确.
正确.
故选:![]() .
.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示,给出四个函数:①
的图象如图所示,给出四个函数:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,又给出四个函数的图象,则正确的匹配方案是( ).
,又给出四个函数的图象,则正确的匹配方案是( ).
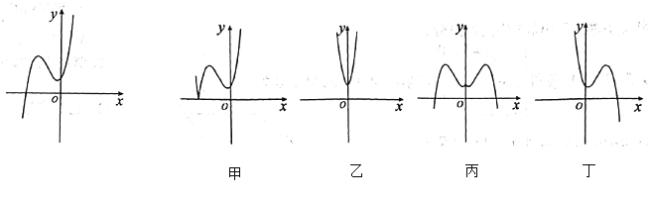
A.①-甲,②-乙,③-丙,④-丁B.②-甲,①-乙,③-丙,④-丙
C.①-甲,③-乙,④-丙,②-丁D.①-甲,④-乙,③-丙,②-丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
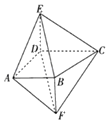
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线C的极坐标方程;
(2)若直线![]() 与直线l相交于点A,与曲线C相交于不同的两点M,N.求
与直线l相交于点A,与曲线C相交于不同的两点M,N.求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
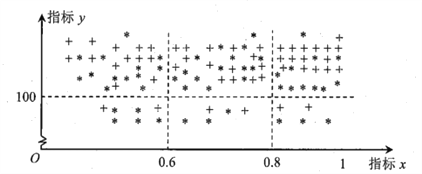
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com