【题目】在极坐标系中，曲线C1：ρsin2θ=4cosθ，以极点为坐标原点，极轴为轴正半轴建立直角坐标系xOy，曲线C2的参数方程为 
（t为参数）．
（1）求C1、C2的直角坐标方程；
（2）若曲线C1与曲线C2交于A、B两点，且定点P的坐标为（2，0），求|PA||PB|的值．
【答案】
（1）解：∵曲线C1：ρsin2θ=4cosθ，∴ρ2sin2θ=4ρcosθ，
∴曲线C1的直角坐标方程为y2=4x．
∵曲线C2的参数方程为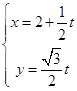 
（t为参数）．
∴曲线C2消去参数t，得曲线C2的直角坐标方程为 
=0．
（2）解：曲线C2的参数方程为 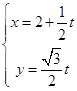（t为参数）代入y2=4x，
得 
=8+2t，即3t2﹣8t﹣32=0，
△=（﹣8）2﹣4×3×（﹣32）=448＞0，
t1t2=﹣ 
，
∴|PA||PB|=|t1||t2|=|t1t2|= ．
【解析】（1）曲线C1的极坐标方程转化为ρ2sin2θ=4ρcosθ，由此能求出曲线C1的直角坐标方程，曲线C2的参数方程消去参数t，能求出曲线C2的直角坐标方程．（2）曲线C2的参数方程代入y2=4x，得3t2﹣8t﹣32=0，由此能求出|PA||PB|的值．
科目：高中数学 来源： 题型：
【题目】设f（x）=lnx，g（x）=f（x）+f′（x）． （Ⅰ）求g（x）的单调区间和最小值；
（Ⅱ）讨论g（x）与 
的大小关系；
（Ⅲ）求a的取值范围，使得g（a）﹣g（x）＜ 
对任意x＞0成立．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正方体ABCD－A1B1C1D1中，E，F分别是线段A1B1，B1C1上的不与端点重合的动点，如果A1E＝B1F，有下面四个结论：
①EF⊥AA1；②EF∥AC；③EF与AC异面；④EF∥平面ABCD.
其中一定正确的有( )
A. ①② B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分14分）
设某旅游景点每天的固定成本为500元，门票每张为30元，变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时，该旅游景点收支平衡；一天购票人数超过100时，该旅游景点须另交保险费200元。设每天的购票人数为
，盈利额为
元。
（Ⅰ）求
与
之间的函数关系；
（Ⅱ）该旅游景点希望在人数达到20人时即不出现亏损，若用提高门票价格的措施，则每张门票至少要多少元（取整数）？
（参考数据：
.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC＝45°，∠BAC＝90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC＝90°.
(1)证明：平面ADB⊥平面BDC；
(2)若BD＝1，求三棱锥D－ABC的表面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正方体ABCD－A1B1C1D1中，E为AB的中点，F为AA1的中点，求证：
(1)E、C、D1、F、四点共面；
(2)CE、D1F、DA三线共点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形ABCD的两条对角线相交于点M(2,0)，AB边所在直线的方程为x－3y－6＝0，点T(－1,1)在AD边所在的直线上．
(1)求AD边所在直线的方程；
(2)求矩形ABCD外接圆的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知菱形 ABCD 中，对角线 AC 与 BD 相交于一点 O，∠A=60°，将△BDC 沿着 BD 折起得△BDC'，连结 AC'． 
（Ⅰ）求证：平面 AOC'⊥平面 ABD；
（Ⅱ）若点 C'在平面 ABD 上的投影恰好是△ABD 的重心，求直线 CD 与底面 ADC'所成角的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
