
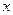
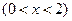 的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.
的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.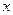 表示);
表示);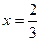 时,Vl取最大值
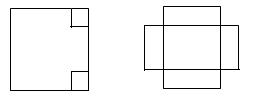
时,Vl取最大值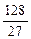 ,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。
,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。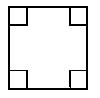


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
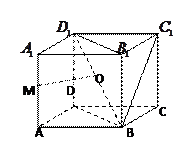
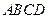 —
—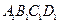 中.
中.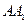 的中点,点
的中点,点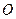 是
是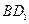 的中点.
的中点.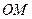 垂直于平面
垂直于平面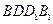 ;
;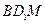 与平面
与平面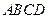 所成二面角的平面角(锐角)
所成二面角的平面角(锐角)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
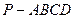 中,底面
中,底面 是矩形,
是矩形,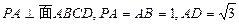 ,点
,点 是
是 的中点,点
的中点,点 在边
在边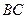 上移动。
上移动。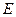 为
为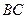 的中点时,试判断
的中点时,试判断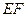 与平面
与平面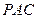 的位置关系,并说明理由。
的位置关系,并说明理由。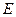 在边
在边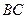 的何处,都有
的何处,都有
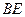 等于何值时,
等于何值时, 与平面
与平面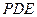 所成角的大小为
所成角的大小为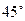 .(12分)
.(12分)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
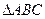 与
与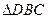 都是边长为
都是边长为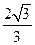 的等边三角形,且平面
的等边三角形,且平面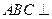 平面
平面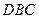 ,过点
,过点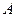 作
作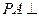 平面
平面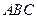 ,且
,且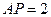 .
.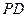 与平面
与平面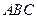 所成角的大小;
所成角的大小;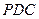 与底面
与底面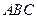 所成的二面角的余弦值.
所成的二面角的余弦值.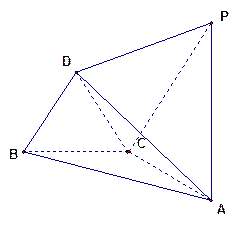
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
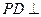 平面
平面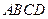 ,
,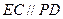 ,且
,且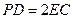 ,
, 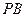 的中点,求证:
的中点,求证: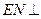 平面
平面 ;
;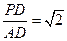 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.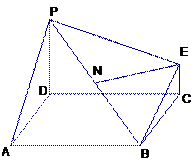
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
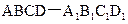 中,M,N,
中,M,N, P分别是
P分别是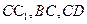 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.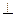 平面
平面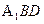 ;
;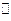 平面
平面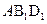 ;
; 的距离
的距离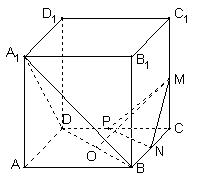
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com