
【题目】圆锥的轴截面是等腰直角三角形,底面半径为1,点![]() 是圆心,过顶点
是圆心,过顶点![]() 的截面
的截面![]() 与底面所成的二面角
与底面所成的二面角![]() 大小是
大小是![]() .
.

(1)求点![]() 到截面
到截面![]() 的距离;
的距离;
(2)点![]() 为圆周上一点,且
为圆周上一点,且![]() ,
,![]() 是
是![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() 对称且过点
对称且过点![]() 和
和![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
(1)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(2)记直线![]() 与圆
与圆![]() 的两个交点为
的两个交点为![]() ,
,![]() .
.
①若弦长![]() ,求实数
,求实数![]() 的值;
的值;
②求![]() 面积的最大值及
面积的最大值及![]() 面积的最大时
面积的最大时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳组的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 | P |
第三组 |
| 100 | 0.5 |
第四组 |
| a | 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
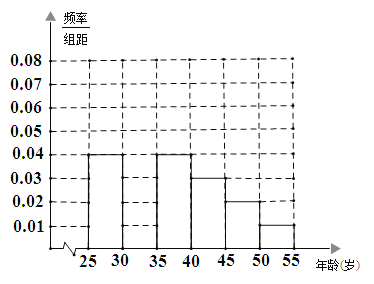
(1)补全频率分布直方图,并求n,a,p的值;
(2)求年龄段人数的中位数和众数;(直接写出结果即可)
(3)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在
岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的电子新产品未上市时,原定每件售价100元,经过市场调研发现,该电子新产品市场潜力很大,该公司决定从第一周开始销售时,该电子产品每件售价比原定售价每周涨价4元,5周后开始保持120元的价格平稳销售,10周后由于市场竞争日益激烈,每周降价2元,直到15周结束,该产品不再销售.
(Ⅰ)求售价![]() (单位:元)与周次
(单位:元)与周次![]() (
(![]() )之间的函数关系式;
)之间的函数关系式;
(Ⅱ)若此电子产品的单件成本![]() (单位:元)与周次
(单位:元)与周次![]() 之间的关系式为
之间的关系式为![]() ,
,![]() ,
,![]() ,试问:此电子产品第几周的单件销售利润(销售利润
,试问:此电子产品第几周的单件销售利润(销售利润![]() 售价
售价![]() 成本)最大?
成本)最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产![]() ,
,![]() 两种产品,根据市场调查与预测,
两种产品,根据市场调查与预测,![]() 产品的利润与投资成正比,其关系如图1,
产品的利润与投资成正比,其关系如图1,![]() 产品的利润与投资的算术平方根成正比,其关系如图2,(注:利润与投资单位:万元)
产品的利润与投资的算术平方根成正比,其关系如图2,(注:利润与投资单位:万元)
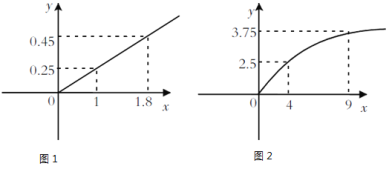
(1)分别将![]() ,
,![]() 两种产品的利润表示为投资的函数关系,并写出它们的函数关系式;
两种产品的利润表示为投资的函数关系,并写出它们的函数关系式;
(2)该企业已筹集到10万元资金,全部投入到![]() ,
,![]() 两种产品的生产,怎样分配资金,才能使企业获得最大利润,其最大利润约为多少万元(精确到1万元).
两种产品的生产,怎样分配资金,才能使企业获得最大利润,其最大利润约为多少万元(精确到1万元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com