
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,![]() ,
,![]() .
.

(Ⅰ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅱ)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,由余弦定理可得;(Ⅱ)设乙步行的速度为 v m/min,从而求出v的取值范围
试题解析:(Ⅰ)∵![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,
,![]()
∴![]()
根据![]() 得
得![]() ,所以乙在缆车上的时间为
,所以乙在缆车上的时间为![]() (min).
(min).
设乙出发![]() (
(![]() )分钟后,甲、乙距离为
)分钟后,甲、乙距离为![]() ,则
,则
![]()
∴![]() 时,即乙出发
时,即乙出发![]() 分钟后,乙在缆车上与甲的距离最短.
分钟后,乙在缆车上与甲的距离最短.
(Ⅱ)由正弦定理![]() 得
得 (m).
(m).
乙从![]() 出发时,甲已经走了50(2+8+1)=550(m),还需走710m才能到达
出发时,甲已经走了50(2+8+1)=550(m),还需走710m才能到达![]() .
.
设乙步行速度为![]()
![]() ,则
,则![]() .解得
.解得![]() .
.
∴为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() 分钟,乙步行的速度应控制在
分钟,乙步行的速度应控制在![]() 范围内.
范围内.


科目:高中数学 来源: 题型:
【题目】在12件同类型的零件中有2件次品,抽取3次进行检验,每次抽取1件,并且取出后不再放回,若以ξ和η分别表示取到的次品数和正品数.
(1)求ξ的分布列、均值和方差;
(2)求η的分布列、均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() :
:![]() 交于点
交于点![]() 两点.
两点.
(1)求![]() 的取值范围;
的取值范围;
(2)请问是否存在实数k使得![]() (其中
(其中![]() 为坐标原点),如果存在请求出k的值,并求
为坐标原点),如果存在请求出k的值,并求![]() ;如果不存在,请说明理由。
;如果不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.
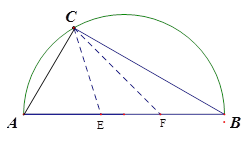
(1)若![]() 米,求
米,求![]() 的长;
的长;
(2)设![]() , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心为坐标原点,其离心率为
的中心为坐标原点,其离心率为![]() ,椭圆
,椭圆![]() 的一个焦点和抛物线
的一个焦点和抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程
的方程![]()
(2)过点![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,试问:在平面上是否存在一个定点
两点,试问:在平面上是否存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,若存在,说出点
,若存在,说出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲,乙两种产品均需用![]() 两种原料,已知生产1吨每种产品需用
两种原料,已知生产1吨每种产品需用![]() 原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com