
分析 不妨取λ=-1,根据x、y的正负去绝对值,将方程化简,得到相应函数在各个区间上的表达式,由此作出函数的图象,即可得出结论.
解答  解:不妨取λ=-1,方程为$\frac{x|x|}{81}+\frac{y|y|}{49}$=-1,图象如图所示.
解:不妨取λ=-1,方程为$\frac{x|x|}{81}+\frac{y|y|}{49}$=-1,图象如图所示.
对于①,不正确,②③⑤,正确
由F(x)=9f(x)+7x=0得f(x)=-$\frac{7}{9}$x.
因为双曲线的渐近线为y=±$\frac{7}{9}$x
所以函数y=f(x)与直线y=-$\frac{7}{9}$x无公共点,
因此F(x)=9f(x)+7x不存在零点,可得④不正确.
故答案为:②③⑤.
点评 本题给出含有绝对值的二次曲线,要我们判断并于曲线性质的几个命题的真假.着重考查了含有绝对值的函数式的化简、函数的图象与性质、直线与圆锥曲线位置关系等知识,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | {4,5} | B. | {2,3} | C. | {1} | D. | {4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{lgx}{2}+\frac{8}{lgx}$ | B. | y=$2\sqrt{{x^2}+2}+\frac{2}{{\sqrt{{x^2}+2}}}$ | ||
| C. | $y=sinx+\frac{4}{sinx}$(0<x<π) | D. | y=ex+4e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
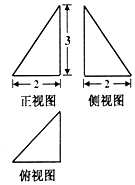 已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.
已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com