
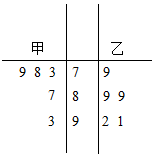
 甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )
甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )| A. | $\overline{x_1}$>$\overline{x_2}$,乙比甲成绩稳定 | B. | $\overline{x_1}$>$\overline{x_2}$,甲比乙成绩稳定 | ||
| C. | $\overline{x_1}$<$\overline{x_2}$,乙比甲成绩稳定 | D. | $\overline{x_1}$<$\overline{x_2}$,甲比乙成绩稳定 |
分析 分别求出甲、乙二人的平均成绩和方差,由此能求出结果.
解答 解:甲的平均成绩$\overline{{x}_{1}}$=$\frac{1}{5}$(73+78+79+87+93)=82,
甲的成绩的方差${{S}_{1}}^{2}$=$\frac{1}{5}$[(73-82)2+(78-82)2+(79-82)2+(87-82)2+(93-82)2]=50.4,
乙的平均成绩$\overline{{x}_{2}}$=$\frac{1}{5}$(79+89+89+92+91)=88,
乙的成绩的方差${{S}_{2}}^{2}$=$\frac{1}{5}$[(79-88)2+(89-88)2+(89-88)2+(92-88)2+(91-88)2]=21.6,
∴$\overline{x_1}$<$\overline{x_2}$,乙比甲成绩稳定.
故选:C.
点评 本题考查甲、乙二人的平均成绩及稳定性的比较,是基础题,解题时要认真审题,注意茎叶图性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,+∞) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1) | C. | (1,2) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{6}}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com