
分析 令f(x)=x3-3,根据用二分法求方程的近似解的方法和步骤,求得方程x3--3=0的近似解(精确度0.1),即为所求.
解答 解:由题意,求f(x)=x3-3的零点即可.
因为f(1)=-2<0,f(2)=5>0,所以方程x3-3=0在区间[1,2]上有实数解,如此下去,
f(1.5)=0.375>0,f(1.25)=-1.05<0,f(1.375)=-0.41<0,f(1.4375)=-0.03<0
至此,我们得到,区间长度为0.0625,它小于0.1.因此,我们可以选取这一区间内的任意一个数作为方程x2-3=0的一个近似解.
例如,可以选取1.4作为方程x2-3=0的一个近似解.
即$\root{3}{3}$的近似值为1.4.
点评 本题主要考查用二分法求方程的近似解的方法和步骤,体现了转化的数学思想,属于基础题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | 6-2$\sqrt{2}$ | B. | 6 | C. | 4+2$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3,4} | B. | {2,3,5} | C. | {3,4,5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
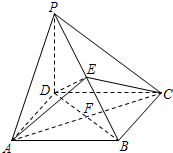 如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com