
【题目】如图①,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图②.
CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图②.
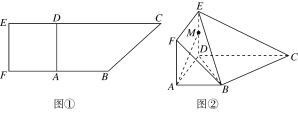
(1)求证:AM∥平面BEC;
(2)求点D到平面BEC的距离.
【答案】(1)证明见解析(2) ![]()
【解析】
取EC的中点为N,连接MN,BN,利用中位线可知四边形ABNM为平行四边形,可得BN∥AM,由线面平行的判定定理即可证明(2)根据又VE-BCD=VD-BCE,由等体积法求出点到面的距离即可.
证明:取EC的中点为N,连接MN,BN.
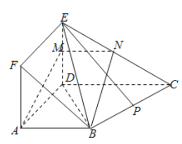
在△EDC中,M,N分别为ED,EC的中点,所以MN∥CD,且MN=![]() CD.由已知AB∥CD,AB=
CD.由已知AB∥CD,AB=![]() CD,得MN∥AB,且MN=AB.故四边形ABNM为平行四边形,因此BN∥AM.
CD,得MN∥AB,且MN=AB.故四边形ABNM为平行四边形,因此BN∥AM.
又因为BN平面BEC,且AM平面BEC,所以AM∥平面BEC.
(2)解:由已知得BC⊥BD,BC⊥DE,又BD∩DE=D,所以BC⊥平面BDE.而BE平面BDE,所以BC⊥BE.
故S△BCE=![]() BE·BC=
BE·BC=![]() ×
×![]() ×
×![]() =
=![]() .
.
S△BCD=![]() BD·BC=
BD·BC=![]() ×
×![]() ×
×![]() =1.
=1.
又VE-BCD=VD-BCE,设点D到平面BEC的距离为h,
则![]() S△BCD·DE=
S△BCD·DE=![]() S△BCE·h,所以h=
S△BCE·h,所以h=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两同学在复习数列时发现原来曾经做过的一道数列问题因纸张被破坏,导致一个条件看不清,具体如下:等比数列![]() 的前n项和为
的前n项和为![]() ,已知_____,
,已知_____,
(1)判断![]() ,
,![]() ,
,![]() 的关系;
的关系;
(2)若![]() ,设
,设![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,证明:
,证明:![]() .
.
甲同学记得缺少的条件是首项a1的值,乙同学记得缺少的条件是公比q的值,并且他俩都记得第(1)问的答案是![]() ,
,![]() ,
,![]() 成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系.xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C2的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了50人就该城市共享单车的推行情况进行问卷调査,并将问卷中的这50人根据其满意度评分值(百分制)按照![]() 分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ▆ |
第3组 |
| 20 | 0.40 |
第4组 |
| ▆ | 0.08 |
第5组 |
| 2 |
|
合计 | ▆ | ▆ |
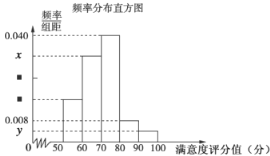
(1)求![]() 的值;
的值;
(2)若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形![]() (图①)中,
(图①)中,![]() 与
与![]() 均为直角三角形且有公共斜边
均为直角三角形且有公共斜边![]() ,设
,设![]() ,∠
,∠![]() ,∠
,∠![]() ,将
,将![]() 沿
沿![]() 折起,构成如图②所示的三棱锥
折起,构成如图②所示的三棱锥![]() ,且使
,且使![]() =
=![]() .
.
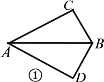
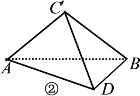
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,四个顶点恰好构成了一个边长为
,四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形.
的菱形.
(1)求椭圆的标准方程;
(2)已知直线![]() ,
,![]() 过右焦点F2,且它们的斜率乘积为
过右焦点F2,且它们的斜率乘积为![]() ,设
,设![]() ,
,![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
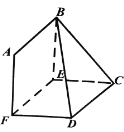
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com