
分析 ①根据逆命题的定义进行判断,
②根据逆命题的定义以及一元二次方程有根的条件进行判断,
③根据逆命题和否命题的等价性进行判断,
④根据逆否命题的定义进行判断.
解答 解:①“等边三角形的三内角均为60°”的逆命题为三内角都是60°的三角形是等边三角形,则逆命题为真命题,故①正确,
②若k>0,则方程x2+2x-k=0有实根“的逆命题为方程x2+2x-k=0有实根,则k>0,
若方程x2+2x-k=0有实根,则判别式△=4+4k≥0,即k≥-1,则k>0不一定成立,故②错误
③“全等三角形的面积相等”的逆命题为面积相等的三角形是全等三角形,为假命题,则命题的否命题也是假命题,故③错误,
④“若ab≠0,则a≠0”的逆否命题是若a=0,则ab=0,为真命题,则命题的逆否命题为真命题,故④正确,
故真命题为①④,
故答案为:2
点评 本题主要考查四种命题的真假判断,利用逆否命题的等价性以及四种命题的定义是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<m<1 | B. | -4<m<4 | C. | -1<m<-2 | D. | -3<m<-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2015)>f(0) | B. | f(2015)<f(0) | C. | f(2015)>e2015•f(0) | D. | f(2015)<e2015•f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)>f(-3) | B. | f(-3)>f(-5) | C. | f(-30.3)>f(0.33) | D. | f(log32)>f(-log23) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
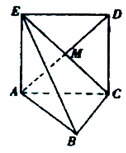 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | [2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com