
【题目】在平面直角坐标系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,求x的值.
,求x的值.
【答案】
(1)解:若 ![]() ⊥
⊥ ![]() ,
,
则 ![]()
![]() =(
=( ![]() ,﹣
,﹣ ![]() )(sinx,cosx)=
)(sinx,cosx)= ![]() sinx﹣
sinx﹣ ![]() cosx=0,
cosx=0,
即 ![]() sinx=
sinx= ![]() cosx
cosx
sinx=cosx,即tanx=1
(2)解:∵| ![]() |=
|= ![]() =1,|
=1,| ![]() |=
|= ![]() =1,
=1, ![]()
![]() =(
=( ![]() ,﹣
,﹣ ![]() )(sinx,cosx)=
)(sinx,cosx)= ![]() sinx﹣
sinx﹣ ![]() cosx,
cosx,
∴若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,
,
则 ![]()
![]() =|
=| ![]() ||
|| ![]() |cos
|cos ![]() =
= ![]() ,
,
即 ![]() sinx﹣
sinx﹣ ![]() cosx=
cosx= ![]() ,
,
则sin(x﹣ ![]() )=
)= ![]() ,
,
∵x∈(0, ![]() ).
).
∴x﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ).
).
则x﹣ ![]() =
= ![]()
即x= ![]() +
+ ![]() =
= ![]()
【解析】(1)若 ![]() ⊥
⊥ ![]() ,则
,则 ![]()
![]() =0,结合三角函数的关系式即可求tanx的值;(2)若
=0,结合三角函数的关系式即可求tanx的值;(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,利用向量的数量积的坐标公式进行求解即可求x的值.
,利用向量的数量积的坐标公式进行求解即可求x的值.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.
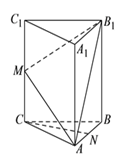
(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长
的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=4
(1)求过点P(3,3)且与圆C相切的直线l的方程;
(2)已知直线m:x﹣y+1=0与圆C交于A、B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2﹣a2= ![]() bc,且b=
bc,且b= ![]() a,则下列关系一定不成立的是( )
a,则下列关系一定不成立的是( )
A.a=c
B.b=c
C.2a=c
D.a2+b2=c2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的倾斜角;
的倾斜角;
(2)设点![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com