已知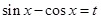
（1）用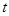 
表示
的值；
（2）求函数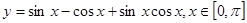
的最大值和最小值．
（参考公式：
）
科目：高中数学 来源： 题型：解答题
受日月引力影响，海水会发生涨退潮现象．通常情况下，船在涨潮时驶进港口，退潮时离开港口．某港口在某季节每天港口水位的深度
（米）是时间
（
，单位：小时，
表示0：00—零时）的函数，其函数关系式为
．已知一天中该港口水位的深度变化有如下规律：出现相邻两次最高水位的深度的时间差为12小时，最高水位的深度为12米，最低水位的深度为6米，每天13：00时港口水位的深度恰为10．5米．
（1）试求函数
的表达式；
（2）某货船的吃水深度（船底与水面的距离）为7米，安全条例规定船舶航行时船底与海底的距离不小于3．5米是安全的，问该船在当天的什么时间段能够安全进港？若该船欲于当天安全离港，则它最迟应在当天几点以前离开港口？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数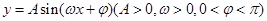
，
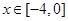时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A，
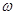和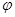
的值；⑵现要在右侧的半圆中修建一条步行道CDO（单位：米），在点C与半圆弧上的一点D之间设计为直线段（造价为2万元/米），从D到点O之间设计为沿半圆弧的弧形（造价为1万元/米）．设
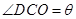(弧度)，试用
来表示修建步行道的造价预算，并求造价预算的最大值？（注：只考虑步行道的长度，不考虑步行道的宽度）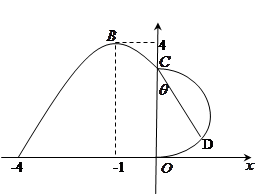
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）最大值为1， 最小值为-1
结合平方关系得，
，可求出
，将
利用辅助角公式化为一个角三角函数，结合所给角的范围和三角函数图像，求出
即
2分
4分
6分
8分
得
10分
且
12分
时，
； 当
时， 
． 14分
在一个周期内，当
时，
取得最小值
；当
时，
;
的周期和单调递增区间；
在
上有解，求实数m的取值范围.
,且
∥
.
; 
.
．
的值；
，求
的值．
，则
=