
【题目】已知函数f(x)= ![]() +
+ ![]() lnx﹣1(m∈R)的两个零点为x1 , x2(x1<x2).
lnx﹣1(m∈R)的两个零点为x1 , x2(x1<x2).
(1)求实数m的取值范围;
(2)求证: ![]() +
+ ![]() >
> ![]() .
.
【答案】
(1)解:f′(x)= ![]() .
.
①m≤0,f′(x)>0,f(x)在(0,+∞)上单调递增,不可能有两个零点;
②m>0,f′(x)>0可解得x>2m,f′(x)<0可解得0<x<2m,
∴f(x)在(0,2m)上单调递减,在(2m,+∞)上单调递增,
∴f(x)min=f(2m)= ![]() ln2m﹣
ln2m﹣ ![]() ,
,
由题意, ![]() ln2m﹣
ln2m﹣ ![]() <0,
<0,
∴0<m< ![]()
(2)证明:令t= ![]() ,f(
,f( ![]() )=mt﹣2lnt﹣1=0,
)=mt﹣2lnt﹣1=0,
由题意方程m= ![]() 有两个根为t1,t2,不妨设t1=
有两个根为t1,t2,不妨设t1= ![]() ,t2=
,t2= ![]() .
.
令h(t)= ![]() ,则h′(t)=﹣
,则h′(t)=﹣ ![]() ,
,
令h′(t)>0,可得0<t< ![]() ,函数单调递增;h′(t)<0,可得t>
,函数单调递增;h′(t)<0,可得t> ![]() ,函数单调递减.
,函数单调递减.
由题意,t1> ![]() >t2>0,
>t2>0,
要证明 ![]() +
+ ![]() >
> ![]() ,即证明t1+t2>
,即证明t1+t2> ![]() ,即证明h(t1)<h(
,即证明h(t1)<h( ![]() ﹣t2).
﹣t2).
令φ(x)=h(x)﹣h( ![]() ﹣x),
﹣x),
下面证明φ(x)<0对任意x∈(0, ![]() )恒成立,
)恒成立,
φ′(x)= ![]() +
+ 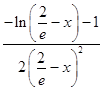 ,
,
∵x∈(0, ![]() ),
),
∴﹣lnx﹣1>0,x2< ![]() ,
,
∴φ′(x)> 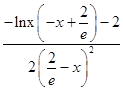 >0,
>0,
∴φ(x)在(0, ![]() )上是增函数,
)上是增函数,
∴φ(x)<φ( ![]() )=0,
)=0,
∴原不等式成立
【解析】(1)求导数,分类讨论,利用函数f(x)= ![]() +
+ ![]() lnx﹣1(m∈R)的两个零点,得出
lnx﹣1(m∈R)的两个零点,得出 ![]() ln2m﹣
ln2m﹣ ![]() <0,即可求实数m的取值范围;(2)由题意方程m=
<0,即可求实数m的取值范围;(2)由题意方程m= ![]() 有两个根为t1 , t2 , 不妨设t1=
有两个根为t1 , t2 , 不妨设t1= ![]() ,t2=
,t2= ![]() ,要证明
,要证明 ![]() +
+ ![]() >
> ![]() ,即证明t1+t2>
,即证明t1+t2> ![]() ,即证明h(t1)<h(
,即证明h(t1)<h( ![]() ﹣t2).令φ(x)=h(x)﹣h(
﹣t2).令φ(x)=h(x)﹣h( ![]() ﹣x),证明φ(x)<0对任意x∈(0,
﹣x),证明φ(x)<0对任意x∈(0, ![]() )恒成立即可.
)恒成立即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】第31届夏季奥林匹克运动会将于2016年8月5日﹣21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
中国 | 38 | 51 | 32 | 28 | 16 |
俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(Ⅰ)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(Ⅱ)甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为 ![]() ,丙猜中国代表团的概率为
,丙猜中国代表团的概率为 ![]() ,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.
,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°. 
(1)求证:平面PBD⊥平面PAC;
(2)求二面角D﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,焦点为F,过点P(﹣1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若 ![]() +
+ ![]() =18,则k= .
=18,则k= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的奇函数,且f(x﹣1)为偶函数,当x∈[0,1]时, ![]() ,若函数g(x)=f(x)﹣x﹣b恰有一个零点,则实数b的取值集合是( )
,若函数g(x)=f(x)﹣x﹣b恰有一个零点,则实数b的取值集合是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ![]() 为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ
为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ
(1)求圆C的直角坐标方程;
(2)若点P(1,2),设圆C与直线l交于点A、B,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和 ![]() ,且a1 , a4是等比数列{bn}的前两项,记bn与bn+1之间包含的数列{an}的项数为cn , 如b1与b2之间包含{an}中的项为a2 , a3 , 则c1=2.
,且a1 , a4是等比数列{bn}的前两项,记bn与bn+1之间包含的数列{an}的项数为cn , 如b1与b2之间包含{an}中的项为a2 , a3 , 则c1=2.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{ancn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+cosx,x∈R.
(1)求函数f(x)的最小正周期和最大值;
(2)函数y=f(x)的图象可由y=sinx的图象经过怎么的变换得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com