
分析 (1)求出函数的导数,解关于导函数的不等式求出函数的单调区间即可;
(2)通过讨论a的范围,判断函数的单调性,求出函数f(x)的最小值,分离参数a,从而求出a的范围.
解答 解:(1)由题意得x∈(0,+∞),
当a=-2时,$f(x)={x^2}-4x-2lnx,f'(x)=\frac{{2{x^2}-4x-2}}{x}=\frac{{2({x-1-\sqrt{2}})({x-1+\sqrt{2}})}}{x}$,…(2分)
∴当$x∈({0,1+\sqrt{2}})$时,f'(x)<0,当$x∈({1+\sqrt{2},+∞})$时,f'(x)>0,…(4分)
∴f(x)的单调减区间是$({0,1+\sqrt{2}})$,单调增区间是$({1+\sqrt{2},+∞})$…(5分)
(2)①当a=0时,f(x)=x2>0,显然符合题意;
②当a<0时,$f'(x)=\frac{{2{x^2}+2ax+a}}{x}$,…(6分)
对于2x2+2ax+a=0,△=4a2-8a>0,
∴该方程有两个不同实根,且一正一负,
即存在x0∈(0,+∞),使得$2x_0^2+2a{x_0}+a=0$,即f'(x0)=0,…(7分)
∴当0<x<x0时,f'(x)<0,当x>x0时,f'(x)>0,…(8分)
∴$f{(x)_{min}}=f({x_0})=x_0^2+2a{x_0}+aln{x_0}=x_0^2+a{x_0}+\frac{a}{2}+({a{x_0}-\frac{a}{2}+aln{x_0}})=a{x_0}-\frac{a}{2}+aln{x_0}$,
∵$f(x)>\frac{1}{2}({2e+1})a$,∴2x0-1+2lnx<2e+1,即x0+lnx0<e+1,
由于g(x)=x+lnx在(0,+∞)上是增函数,
∴0<x0<e…(9分)
由$2x_0^2+2a{x_0}+a=0$得$a=-\frac{2x_0^2}{{2{x_0}+1}}$,
设$h(x)=-\frac{{2{x^2}}}{2x+1}$,则$h'(x)=-\frac{{4{x^2}+4x}}{{{{({2x+1})}^2}}}<0$,
∴函数$h(x)=-\frac{{2{x^2}}}{2x+1}$在(0,e)上单调递减,…(10分)
∴$-\frac{2x_0^2}{{2{x_0}+1}}∈({-\frac{{2{e^2}}}{2e+1},0})$…(11分)
综上所述,实数a的取值范围$({-\frac{{2{e^2}}}{2e+1},0}]$…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
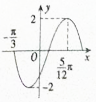 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
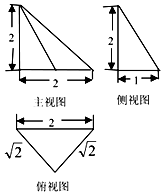
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com