
 ,由此归纳出{an}的通项公式
,由此归纳出{an}的通项公式 ,通过计算a2,a3,a4由此归纳出{an}的通项公式,是归纳推理.
,通过计算a2,a3,a4由此归纳出{an}的通项公式,是归纳推理.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:2012届山东省兖州市高二下学期期末考试数学(文) 题型:选择题
下列推理过程属于演绎推理的为( )
A.老鼠、猴子与人在身体结构上有相似之处,某医药先在猴子身上试验,试验成功后再用于人体试验
B.由 得出
得出

C.由三角形的三条中线交于一点联想到四面体四条中线(四面体每一个顶点与对面重心的连线)交于一点
D.通项公式形如 的数列
的数列 为等比数列,则数列
为等比数列,则数列 为等比数列
为等比数列
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省济宁市兖州市高二(下)期末数学试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省兖州市高二下学期期末考试数学(文) 题型:单选题
下列推理过程属于演绎推理的为( )
A.老鼠、猴子与人在身体结构上有相似之处,某医药先在猴子身上试验,试验成功后再用于人体试验
B.由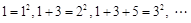 得出
得出

C.由三角形的三条中线交于一点联想到四面体四条中线(四面体每一个顶点与对面重心的连线)交于一点
D.通项公式形如 的数列
的数列 为等比数列,则数列
为等比数列,则数列 为等比数列
为等比数列
查看答案和解析>>
科目:高中数学 来源:广东省潮州金中08-09学年高二下学期期中考试(理) 题型:选择题
下列命题中,正确的命题为
A.合情推理就是正确的推理 B.归纳推理是从一般到特殊的推理过程
C.类比推理是从特殊到一般的推理过程 D.演绎推理是一般到特殊的推理过程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com