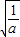函数f(x)=1-ax2(a>0,x>0),该函数图象在点P(x,1-ax2) 处的切线为l,设切线l 分别交x 轴和y 轴于两点M和N.
(1)将△MON (O 为坐标原点)的面积S 表示为x 的函数S(x);
(2)若在x=1处,S(x)取得最小值,求此时a的值及S(x)的最小值;
(3)若记M点的坐标为M(m,0),函数y=f(x) 的图象与x轴交于点T(t,0),则m与t的大小关系如何?证明你的结论.
【答案】
分析:(1)根据道说的几何意义可得函数图象在点P(x
,1-ax
2) 处的切线的斜率为f
′(x
)=-2ax
再由点斜式写出切线方程然后根据题意易得M,N的坐标再根据面积公式
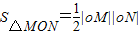
即可得解.
(2)在第一问的基础上可利用
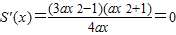
判断出s(x
)的单调性然后根据单调性可得出S(x
)的最小值以及取得最小值时a的值.
(3)求出t的值结合(1)得m=
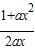
再结合t的值将m拆成和的形式在利用基本不等式进行放缩即可得解.
解答:解:(1)∵f(x)=1-ax
2(a>0,x>0)
∴f
′(x)=-2ax
∴f
′(x
)=-2ax
∴函数图象在点P(x
,1-ax
2) 处的切线为y-(1-ax
2)=-2ax
(x-x
)即y=-2ax
x+1+ax
2∴M(
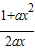
,0),N(0.1+ax
2)
∴
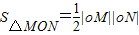
=
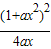
(2)令
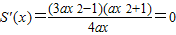
则
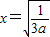
∴当0<x
<
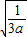
时s
′(x
)<0则s(x
)单调递减
当
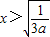
时s
′(x
)>0则s(x
)单调递增
∴
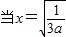
=1 时,面积最小此时
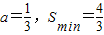
(3)由题意知t=
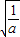
又∵m=
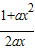
=
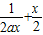
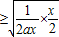
=
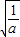
∴m≥t
点评:本题主要考查了导数的应用.解题的关键是第一问要知道在某一点出切线的斜率即为在这一点处的导数,而第二问要利用导数判断函数S(x
)的单调性进而求其最小值,第三问关键是将m拆成和的形式在利用基本不等式进行放缩.

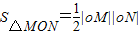 即可得解.
即可得解.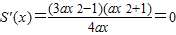 判断出s(x)的单调性然后根据单调性可得出S(x)的最小值以及取得最小值时a的值.
判断出s(x)的单调性然后根据单调性可得出S(x)的最小值以及取得最小值时a的值.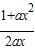 再结合t的值将m拆成和的形式在利用基本不等式进行放缩即可得解.
再结合t的值将m拆成和的形式在利用基本不等式进行放缩即可得解.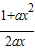 ,0),N(0.1+ax2)
,0),N(0.1+ax2)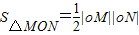 =
=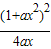
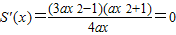
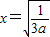
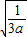 时s′(x)<0则s(x)单调递减
时s′(x)<0则s(x)单调递减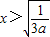 时s′(x)>0则s(x)单调递增
时s′(x)>0则s(x)单调递增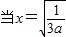 =1 时,面积最小此时
=1 时,面积最小此时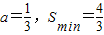
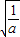
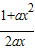 =
=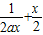
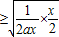 =
=