
 +
+ =1 的左、右焦点,三个内角A、B、C满足sinA-sinB=
=1 的左、右焦点,三个内角A、B、C满足sinA-sinB= sinC,则顶点C的轨迹方程是
sinC,则顶点C的轨迹方程是 -
-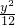 =1
=1 -
-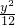 =1 (x<0)
=1 (x<0) -
-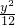 =1 (x<-2 )
=1 (x<-2 ) -
-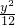 =1
=1 sinC化为|BC|-|AC|=
sinC化为|BC|-|AC|= |AB|,从而判断顶点C是以A、B为焦点的双曲线的左支(除掉与x轴的交点),根据已知条件求出相关量即可求得方程.
|AB|,从而判断顶点C是以A、B为焦点的双曲线的左支(除掉与x轴的交点),根据已知条件求出相关量即可求得方程. +
+ =1 的左、右焦点,所以A(-4,0),B(4,0),
=1 的左、右焦点,所以A(-4,0),B(4,0), =2R(R为△ABC外接圆的半径),
=2R(R为△ABC外接圆的半径), sinC,得
sinC,得 ,即|BC|-|AC|=
,即|BC|-|AC|= |AB|=4<|AB|,
|AB|=4<|AB|, =1(x<-a),
=1(x<-a), .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△ABC的两个顶点A、B分别是椭圆![]() 的左、右焦点, 三个内角A、B、C满足
的左、右焦点, 三个内角A、B、C满足![]() , 则顶点C的轨迹方程是( ).
, 则顶点C的轨迹方程是( ).
A. ![]() B.
B. ![]() (x<0) C.
(x<0) C. ![]() (x.<-2 ) D.
(x.<-2 ) D. ![]()
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x2 |
| 25 |
| y2 |
| 9 |
| 1 |
| 2 |
A.
| B.
| ||||||||
C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市宁海县知恩中学高二(上)12月段考数学试卷(文科)(解析版) 题型:选择题
 +
+ =1 的左、右焦点,三个内角A、B、C满足sinA-sinB=
=1 的左、右焦点,三个内角A、B、C满足sinA-sinB= sinC,则顶点C的轨迹方程是( )
sinC,则顶点C的轨迹方程是( ) -
- =1
=1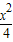 -
- =1 (x<0)
=1 (x<0) -
- =1 (x<-2 )
=1 (x<-2 ) -
- =1
=1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com