
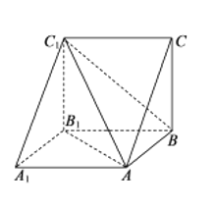
【题目】《九章算术》中记载:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱剖开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵![]() 中,
中,![]() 且有鳖臑C1-ABB1和鳖臑
且有鳖臑C1-ABB1和鳖臑![]() ,现将鳖臑
,现将鳖臑![]() 沿线BC1翻折,使点C与点B1重合,则鳖臑
沿线BC1翻折,使点C与点B1重合,则鳖臑![]() 经翻折后,与鳖臑
经翻折后,与鳖臑![]() 拼接成的几何体的外接球的表面积是______.
拼接成的几何体的外接球的表面积是______.
科目:高中数学 来源: 题型:
【题目】当急需住院人数超过医院所能收治的病人数量时就会发生“医疗资源挤兑”现象,在新冠肺炎爆发期间,境外某市每日下班后统计住院人数,从中发现:该市每日因新冠肺炎住院人数均比前一天下班后统计的住院人数增加约25%,但每日大约有200名新冠肺炎患者治愈出院,已知该市某天下班后有1000名新冠肺炎患者住院治疗,该市的医院共可收治4000名新冠肺炎患者,若继续按照这样的规律发展,该市因新冠肺炎疫情发生“医疗资源挤兑”现象,只需要约( )
参考数据:![]() .
.
A.7天B.10天C.13天D.16天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比到直线
的距离比到直线![]() 的距离小
的距离小![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)过点![]() 且倾斜角为
且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)设![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() ,是否存在垂直于
,是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中的数形结合也可以组成世间万物的绚丽画面,一些优美的曲线是数学形象美、对称美、和谐美的产物,曲线![]() 为四叶玫瑰线,下列结论正确的有( )
为四叶玫瑰线,下列结论正确的有( )
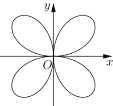
(1)方程![]() (
(![]() ),表示的曲线在第二和第四象限;
),表示的曲线在第二和第四象限;
(2)曲线![]() 上任一点到坐标原点
上任一点到坐标原点![]() 的距离都不超过2;
的距离都不超过2;
(3)曲线![]() 构成的四叶玫瑰线面积大于
构成的四叶玫瑰线面积大于![]() ;
;
(4)曲线![]() 上有5个整点(横、纵坐标均为整数的点);
上有5个整点(横、纵坐标均为整数的点);
A.(1)(2)B.(1)(2)(3)
C.(1)(2)(4)D.(1)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若曲线![]() 在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
(3)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系.xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C2的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农业银行广元分行发行“金穗广元·剑门关旅游卡”是以“游广元、知广元、爱广元、共享和谐广元”为主题活动的一项经济性和公益性相结合的重大举措,以最优惠的价格惠及广元户籍市民、浙江及黑龙江援建省群众、省内援建市市民,凡上述对象均可办理此卡,本人凭此卡及本人身份证一年内(期满后可重新充值办理)在广元市范围内可无限次游览所有售门票景区景点,如:剑门关、朝天明月峡、旺苍鼓城山—七里峡、青川唐家河、广元皇泽寺、苍溪梨博园、昭化古城等,现有浙江及黑龙江援建省群众甲乙两人准备到广元旅游(同游),他们决定游览上面![]() 个景点,首先游览剑门关但不能最后游览朝天明月峡的游览顺序有( )种.
个景点,首先游览剑门关但不能最后游览朝天明月峡的游览顺序有( )种.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com