
【题目】一个摸球游戏,规则如下:在一不透明的纸盒中,装有6个大小相同、颜色各异的玻璃球.参加者交费1元可玩1次游戏,从中有放回地摸球3次.参加者预先指定盒中的某一种颜色的玻璃球,然后摸球.当所指定的玻璃球不出现时,游戏费被没收;当所指定的玻璃球出现1次,2次,3次时,参加者可相应获得游戏费的0倍,1倍,![]() 倍的奖励(
倍的奖励(![]() ),且游戏费仍退还给参加者.记参加者玩1次游戏的收益为
),且游戏费仍退还给参加者.记参加者玩1次游戏的收益为![]() 元.
元.
(1)求概率![]() 的值;
的值;
(2)为使收益![]() 的数学期望不小于0元,求
的数学期望不小于0元,求![]() 的最小值.
的最小值.
(注:概率学源于赌博,请自觉远离不正当的游戏!)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数,
为参数,![]() 为
为![]() 的倾斜角,且
的倾斜角,且![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为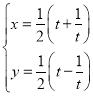 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,曲线
,曲线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在集合![]() 中,任取
中,任取![]() 个元素构成集合
个元素构成集合![]() . 若
. 若![]() 的所有元素之和为偶数,则称
的所有元素之和为偶数,则称![]() 为
为![]() 的偶子集,其个数记为
的偶子集,其个数记为![]() ;若
;若![]() 的所有元素之和为奇数,则称
的所有元素之和为奇数,则称![]() 为
为![]() 的奇子集,其个数记为
的奇子集,其个数记为![]() . 令
. 令![]()
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
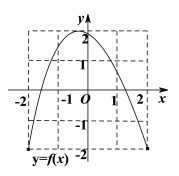
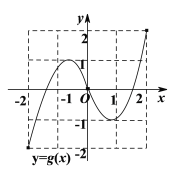
【题目】如图分别为定义域和值域均为![]() 的函数
的函数![]() 和函数
和函数![]() 的图象,则下列命题正确的是( )
的图象,则下列命题正确的是( )
A.函数![]() 恰有
恰有![]() 个零点B.函数
个零点B.函数![]() 恰有
恰有![]() 个零点
个零点
C.函数![]() 恰有
恰有![]() 个零点D.函数
个零点D.函数![]() 恰有
恰有![]() 个零点
个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人玩摸球游戏,每两局为一轮,每局游戏的规则如下:甲,乙两人均从装有4只红球、1只黑球的袋中轮流不放回摸取1只球,摸到黑球的人获胜,并结束该局.
(1)若在一局中甲先摸,求甲在该局获胜的概率;
(2)若在一轮游戏中约定:第一局甲先摸,第二局乙先摸,每一局先摸并获胜的人得1分,后摸井获胜的人得2分,未获胜的人得0分,求此轮游戏中甲得分X的概率分布及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com