
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 的切线方程;
的切线方程;
(2)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,试讨论
时,试讨论![]() 在
在![]() 内的极值点的个数.
内的极值点的个数.
【答案】(1) ![]() ;(2)实数
;(2)实数![]() 的取值范围为
的取值范围为![]() ;
;
(3)当![]() ,
, ![]() 在
在![]() 内的极值点的个数为1;当
内的极值点的个数为1;当![]() 时,
时, ![]() 在
在
![]() 内的极值点的个数为0.
内的极值点的个数为0.
【解析】试题分析:(1)利用导数的几何意义求曲线在点![]() 处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率
处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率![]() ,最后把直线方程化成一般式;(2)利用导数方法证明不等式
,最后把直线方程化成一般式;(2)利用导数方法证明不等式![]() 在区间
在区间![]() 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数![]() ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数![]() ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数![]() 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式;(3)对于恒成立的问题常采用分离参数的方法,常用到两个结论:(1)
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式;(3)对于恒成立的问题常采用分离参数的方法,常用到两个结论:(1)![]() ,(2)
,(2)![]() ;(4)单调函数最多只有一个零点.
;(4)单调函数最多只有一个零点.
试题解析:解:(1) 由题意知![]() ,所以
,所以![]()
又![]() ,
, ![]()
所以曲线![]() 在点
在点![]() 的切线方程为
的切线方程为![]() 5分
5分
(2)由题意:![]()
![]() ,即
,即![]()
设![]() ,则
,则![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
所以当![]() 时,
时, ![]() 取得最大值
取得最大值![]()
故实数![]() 的取值范围为
的取值范围为![]() . 10分
. 10分
(3) ![]() ,
,![]() ,
,![]()
①当![]() 时, ∵
时, ∵ ∴存在
∴存在![]() 使得
使得![]()
因为![]() 开口向上,所以在
开口向上,所以在![]() 内
内![]() ,在
,在![]() 内
内![]() 即
即![]() 在
在![]() 内是增函数,
内是增函数, ![]() 在
在![]() 内是减函数
内是减函数
故![]() 时,
时, ![]() 在
在![]() 内有且只有一个极值点, 且是极大值点. 12分
内有且只有一个极值点, 且是极大值点. 12分
②当![]() 时,因
时,因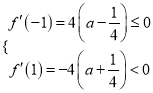
又因为![]() 开口向上
开口向上
所以在![]() 内
内![]() 则
则![]() 在
在![]() 内为减函数,故没有极值点 14分
内为减函数,故没有极值点 14分
综上可知:当![]() ,
, ![]() 在
在![]() 内的极值点的个数为1;当
内的极值点的个数为1;当![]() 时,
时, ![]() 在
在
![]() 内的极值点的个数为0. 15分
内的极值点的个数为0. 15分


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数y=f(x),当x≥0时,f(x)=x2﹣2x. 
(1)求当x<0时,函数y=f(x)的解析式,并在给定坐标系下,画出函数y=f(x)的图象;
(2)写出函数y=|f(x)|的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为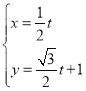 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算题
(1)已知集合A={x|3<x<7},B={x|2<x<10},求A∪B,A∩B,RA
(2)计算下列各式 ① ![]()
②(2a ![]() b
b ![]() )(﹣6a
)(﹣6a ![]() b
b ![]() )÷(﹣3a
)÷(﹣3a ![]() b
b ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=3x , h(x)=9x .
(1)解方程:h(x)﹣8g(x)﹣h(1)=0;
(2)令p(x)= ![]() ,求值:p(
,求值:p( ![]() )+p(
)+p( ![]() )+…+p(
)+…+p( ![]() )+p(
)+p( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某消防机构为![]() 四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
小区 | A | B | C | D |
代表人数 | 45 | 60 | 30 | 15 |
(I)求此活动中各小区“幸运之星”的人数;
(II)从B小区和C小区的“幸运之星”中任选两人进行后续的活动,求这两个人均来自B小区的概率;
(III)消防机构在B小区内,对参加问答活动的居民进行了是否有兴趣参加消防安全培训的问卷调查,统计结果如下(单位:人):
有兴趣 | 无兴趣 | 合计 | |
男 | 25 | 5 | 30 |
女 | 15 | 15 | 30 |
合计 | 40 | 20 | 60 |
据此判断能否在犯错误的概率不超过![]() 的前提下认为有兴趣参加消防安全培训与性别有关系?
的前提下认为有兴趣参加消防安全培训与性别有关系?
临界值表:
|
|
|
|
|
|
|
|
|
|
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com