
【题目】已知函数f(x)的定义域为(﹣1,1),对任意x,y∈(﹣1,1),有f(x)+f(y)=f( ![]() ).且当x<0时,f(x)>0.
).且当x<0时,f(x)>0.
(1)验证函数f(x)=lg ![]() 是否满足这些条件;
是否满足这些条件;
(2)若f( ![]() )=1,f(
)=1,f( ![]() )=2,且|a|<1,|b|<1,求f(a),f(b)的值.
)=2,且|a|<1,|b|<1,求f(a),f(b)的值.
(3)若f(﹣ ![]() )=1,试解关于x的方程f(x)=﹣
)=1,试解关于x的方程f(x)=﹣ ![]() .
.
【答案】
(1)解:由 ![]() 可得﹣1<x<1,即其定义域为(﹣1,1)
可得﹣1<x<1,即其定义域为(﹣1,1)
又 ![]() =
= 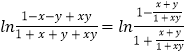 =
= ![]()
又当x<0时,1﹣x>1+x>0,∴ ![]() ∴
∴ ![]()
故 ![]() 满足这些条件
满足这些条件
(2)解:令x=y=0,∴f(0)=0,
令y=﹣x,有f(﹣x)+f(x)=f(0)=0,∴f(x)为奇函数
由条件得 ![]() ,解得
,解得 ![]()
(3)解:设﹣1<x1<x2<1,则x1﹣x2<0,1﹣x1x2>0, ![]() ,
,
则 ![]() ,f(x1)﹣f(x2)>0,∴f(x)在(﹣1,1)上是减函数
,f(x1)﹣f(x2)>0,∴f(x)在(﹣1,1)上是减函数
∵ ![]()
原方程即为 ![]() ,
,
∴ ![]()
又∵ ![]()
故原方程的解为 ![]()
【解析】(1)先求定义域看其是否满足条件,然后验证函数是否满足 ![]() ,最后求出当x<0时的值域,看是否满足即可;(2)先判定函数的奇偶性,然后
,最后求出当x<0时的值域,看是否满足即可;(2)先判定函数的奇偶性,然后 ![]() 建立f(a),f(b)的方程组,解之即可;(3)先判定函数f(x)在(﹣1,1)上的单调性,然后得到
建立f(a),f(b)的方程组,解之即可;(3)先判定函数f(x)在(﹣1,1)上的单调性,然后得到 ![]() ,建立关于x的方程,解之即可.
,建立关于x的方程,解之即可.
【考点精析】关于本题考查的函数的值,需要了解函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能得出正确答案.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】定义:在平面内,点![]() 到曲线
到曲线![]() 上的点的距离的最小值称为点
上的点的距离的最小值称为点![]() 到曲线
到曲线![]() 的距离,在平面直角坐标系
的距离,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
: ![]() 及点
及点![]() ,动点
,动点![]() 到圆
到圆![]() 的距离与到
的距离与到![]() 点的距离相等,记
点的距离相等,记![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过原点的直线![]() (
(![]() 不与坐标轴重合)与曲线
不与坐标轴重合)与曲线![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,设直线
,设直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,|φ|< ![]() )的图象如图所示,为了得到g(x)=sin(2x+
)的图象如图所示,为了得到g(x)=sin(2x+ ![]() )的图象,则只需将f(x)的图象( )
)的图象,则只需将f(x)的图象( ) 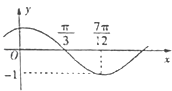
A.向右平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校对甲、乙两个班级进行了物理测验,成绩统计如下(每班50人):
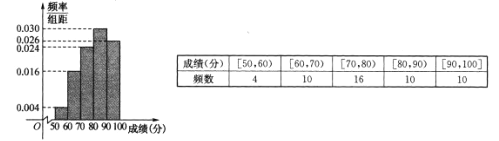
(1)估计甲班的平均成绩;
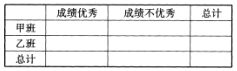
(2)成绩不低于80分记为“优秀”.请完成下面的![]() 列联表,并判断是否有85%的把握认为:“成绩优秀”与所在教学班级有关?
列联表,并判断是否有85%的把握认为:“成绩优秀”与所在教学班级有关?
(3)从两个班级,成绩在![]() 的学生中任选2人,记事件
的学生中任选2人,记事件![]() 为“选出的2人中恰有1人来自甲班”.求事件
为“选出的2人中恰有1人来自甲班”.求事件![]() 的概率
的概率![]() .
.
附: 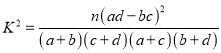
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取3个点,记落在直线![]() 右下方的点的个数为
右下方的点的个数为![]() ,求
,求![]() 的分布列以及期望.
的分布列以及期望.
参考公式: 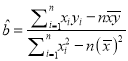 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x﹣1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com