
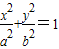 (a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形.
(a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形. ).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;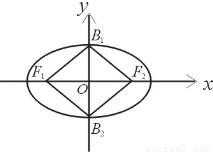
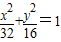 .由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须
.由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须 ,利用方程的根与系数的关系代入得
,利用方程的根与系数的关系代入得 ,从而可求k得范围
,从而可求k得范围 .∴所求椭圆方程为
.∴所求椭圆方程为 .
. .
.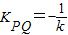
 ,
,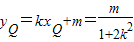
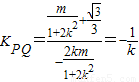
 .③
.③
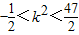 ,
,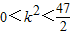
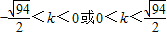 ..
..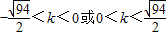 时,A、B两点关于过点P、Q的直线对称.
时,A、B两点关于过点P、Q的直线对称.

科目:高中数学 来源: 题型:
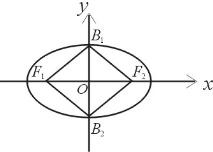 如图椭圆G:
如图椭圆G:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
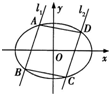 (2012•海淀区一模)在平面直角坐标系xOy中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),P为椭圆G的上顶点,且∠PF1O=45°.
(2012•海淀区一模)在平面直角坐标系xOy中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),P为椭圆G的上顶点,且∠PF1O=45°.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市鱼台一中高二(上)期末数学模拟试卷(理科)(解析版) 题型:解答题
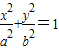 (a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形.
(a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形.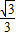 ).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷B(五)(解析版) 题型:解答题
 在平面直角坐标系xOy中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),P为椭圆G的上顶点,且∠PF1O=45°.
在平面直角坐标系xOy中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),P为椭圆G的上顶点,且∠PF1O=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com