练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．定义在R上的函数f（x）满足：对于任意x，都有f（x）=f（x-1）+f（x+1），则f（x）的一个周期为6．

    分析 由已知中f（x）=f（x-1）+f（x+1），可得f（x+6）=f（x），进而得到答案．

    解答 解：∵定义在R上的函数f（x）满足：对于任意x，都有f（x）=f（x-1）+f（x+1），
    用x-1替换x，可得：f（x-1）=f（x-2）+f（x），
    故f（x+1）=-f（x-2），
    ∴f（x+6）=f[（x+5）+1）=-f[（x+5）-2]=-f（x+3）=-f[（x+2）+1）=f[（x+2）-2]=f（x），
    故f（x）的一个周期为6，
    故答案为：6

    点评 本题考查的知识点是函数的周期性，根据已知得到f（x+6）=f（x），是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．经过点A（$\sqrt{3}$，-1），且倾斜角为60°的直线方程为（　　）
    A．$\sqrt{3}$x-y-4=0B．$\sqrt{3}$x+y-2=0C．$\sqrt{3}$x-y-2=0D．$\sqrt{3}$x+y-4=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设向量$\overrightarrow{OA}=（5+cosθ，4+sinθ）$，$\overrightarrow{OB}=（2，0）$，则$|\overrightarrow{AB}|$的取值范围是[4，6]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

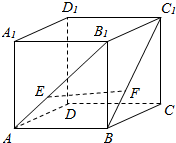    1．如图，正方体ABCD-A1B1C1D1，E，F分别在AB1，BC1上，且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2，过EF做一个平面和面ABCD相交，并找到交线，写出作法．（注意：交线必须是由两个确定的点的连线）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率为$\frac{1}{2}$．过原点的直线与椭圆C交于A、B两点（A，B不是椭圆C的顶点），点D在椭圆C上，且AD⊥AB．
    （1）求椭圆C的右准线方程为：x=4．求椭圆C的方程；
    （2）设直线BD、AB的斜率分别为k1，k2，求$\frac{{k}_{1}}{{k}_{2}}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=4x-2x+1+2，x∈R．
    （1）当x∈[-1，2]时，求f（x）的值域．
    （2）记（1）中的f（x）的值域为集合A，若关于x的方程x2-（a+1）x+a+1=0在x∈A上有解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需要维修），其他三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米），修建此矩形场地围墙的总费用为y（单位：元）．
    （1）将y表示为x的函数；
    （2）写出函数f（x）=y的单调区间，并证明；
    （3）根据（2），试确定x，试修建此矩形场地围墙的总费用最小，并求出最小总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-2x，x＞1}\\{kx-2，x≤1}\end{array}\right.$是定义在R上的增函数，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知f（x）是偶函数，且x≥0时，f（x）=3x，则f（-2）=9．

    查看答案和解析>>

    同步练习册答案