
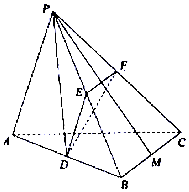
 如图,已知三棱锥P-ABC,BC⊥AC,BC=AC=2,PA=PB,平面PAB⊥平面ABC,D、E、F分别是AB、PB、PC的中点.
如图,已知三棱锥P-ABC,BC⊥AC,BC=AC=2,PA=PB,平面PAB⊥平面ABC,D、E、F分别是AB、PB、PC的中点.分析 (Ⅰ)由PA=PB,D为AB中点,可得PD⊥AB,再由面面垂直的性质可得PD⊥平面ABC;
(Ⅱ)设PM交EF于N,连接DM,DN,由线面垂直的性质得到PM⊥DN,由已知可得DN垂直平分PM,故PD=DM,求出DM,进一步求得PD.即三棱锥P-ABC的高,然后由三棱锥体积公式求得三棱锥P-ABC的体积.
解答 (Ⅰ)证明:∵PA=PB,D为AB中点,∴PD⊥AB,
又平面PAB⊥平面ABC,交线为AB,PD?平面PAB,
∴PD⊥平面ABC;
(Ⅱ)解:设PM交EF于N,连接DM,DN,
∵PM⊥平面EFD,DN?平面DEF,
∴PM⊥DN,
又E,F分别是PB,PC的中点,
∴N为EF的中点,也是PM的中点,
∴DN垂直平分PM,故PD=DM,
又DM为△ABC的中位线,则DM=$\frac{1}{2}AC$=1,∴PD=1.
∵BC⊥AC,则${S}_{△ABC}=\frac{1}{2}AC•BC=2$.
∴三棱锥P-ABC的体积${V}_{P-ABC}=\frac{1}{3}{S}_{△ABC}•PD=\frac{2}{3}$
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了多面体体积的求法,是中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{5}$个单位长度 | B. | 向右平行移动$\frac{π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{10}$个单位长度 | D. | 向右平行移动$\frac{π}{10}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$) | B. | [$\frac{1}{3}$,$\frac{1}{e}$) | C. | ($\frac{1}{e}$,$\frac{4}{3}$] | D. | (-∞,0]∪[$\frac{4}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com