
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2 |
| 3 |
| y2 |
| 2 |
|
| 6k |
| 3k2+2 |
| x1+x2 |
| 2 |
| 3k |
| 3k2+2 |
| 2 |
| 3k2+2 |
| 1 |
| k |
| 2 |
| 3k2+2 |
| 1 |
| k |
| 3k |
| 3k2+2 |
| k |
| 3k2+2 |
| k |
| 3k2+2 |
| k |
| 3k2+2 |
| 1 | ||
3k+
|
| 1 | ||||
2
|
| ||
| 12 |
| ||
| 12 |
| k |
| 3k2+2 |
| 1 | ||
3k+
|
| 1 | ||||
2
|
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
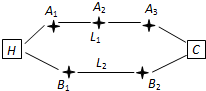 (2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为
(2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省哈师大附中下学期高二期末考试数学试题(文科) 题型:填空题
(2011•丰台区一模)将全体正奇数排成一个三角形数阵:
1
3 5
7 9 11
13 15 17 19
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3个数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com