
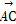 =c,
=c,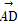 =d,则
=d,则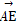 = (用c与d表示).
= (用c与d表示).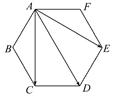
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:不详 题型:填空题
 ,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,
,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点, ,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).
,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =α
=α +β
+β ,其中α,β∈R且α+β=1,则点C的轨迹方程为( )
,其中α,β∈R且α+β=1,则点C的轨迹方程为( )| A.(x-1)2+(y-2)2=5 | B.3x+2y-11=0 |
| C.2x-y=0 | D.x+2y-5=0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =λa+b,
=λa+b, =a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )
=a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )| A.λ+μ=2 | B.λ-μ=1 |
| C.λμ=-1 | D.λμ=1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
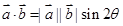 ,(其中
,(其中 为
为 、
、 的夹角),已知△ABC中,
的夹角),已知△ABC中,
 ,则此三角形一定是( )
,则此三角形一定是( )| A.等腰三角形 | B.直角三角形 | C.锐角三角形 | D.钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com