
已知函数 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
 | 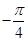 |  |  |  | 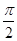 |  |
 |  | 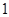 |  |  | 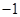 |  |
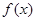 的解析式;
的解析式;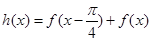 ,
,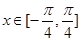 ,求
,求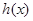 的最大值和最小值.
的最大值和最小值. (Ⅰ)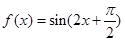 (或者
(或者 );(Ⅱ)
);(Ⅱ)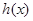 的最大值是2,最小值是
的最大值是2,最小值是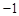 .
.
解析试题分析:(Ⅰ)现根据表格数据的特点求最小正周期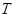 ,再利用公式
,再利用公式 求出
求出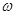 的值,然后再找图象的最高点或最低点或对称中心点确定
的值,然后再找图象的最高点或最低点或对称中心点确定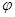 的值,这样便求出了函数
的值,这样便求出了函数 的解析式;(Ⅱ)先确定函数
的解析式;(Ⅱ)先确定函数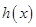 的解析式
的解析式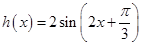 ,然后利用复合函数以及正弦函数的图象确定函数
,然后利用复合函数以及正弦函数的图象确定函数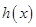 在区间
在区间 上的最小值与最大值,具体做法时,令
上的最小值与最大值,具体做法时,令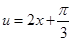 ,根据
,根据 的范围确定
的范围确定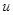 的取值范围
的取值范围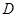 ,然后利用正弦函数
,然后利用正弦函数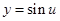 的图象确定
的图象确定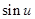 在区间
在区间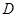 上的最值,进而求出函数数
上的最值,进而求出函数数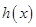 在区间
在区间 上的最小值与最大值.
上的最小值与最大值.
试题解析:解:(Ⅰ)由表格给出的信息可以知道,函数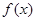 的周期为
的周期为 ,
,
所以 .由
.由 ,且
,且 ,得
,得 . 4分
. 4分
所以函数解析式为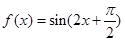 (或者
(或者 ). 6分
). 6分
(Ⅱ)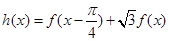

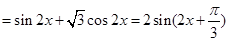 , 9分
, 9分
又因为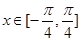 ,所以
,所以 ,所以
,所以 ,
,
所以函数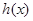 的最大值是2,最小值是
的最大值是2,最小值是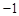 . 12分
. 12分
考点:三角函数的周期、对称性、最值、辅助角变换


科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度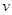 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度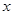 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度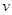 是车流密度
是车流密度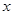 的一次函数.
的一次函数.
(Ⅰ)当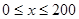 时,求函数
时,求函数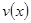 的表达式;
的表达式;
(Ⅱ)当车流密度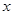 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)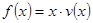 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
国家助学贷款是由财政贴息的信用贷款(即无利息贷款),旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2013届毕业生小王在本科期间共申请了24000元助学贷款,并承诺在毕业后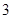 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第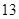 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加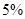 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多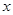 元.
元.
(1)假设小王在第 个月还清贷款(
个月还清贷款(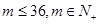 ),试用
),试用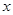 和
和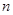 表示小王第
表示小王第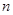 (
(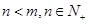 )个月的还款额
)个月的还款额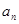 ;
;
(2)当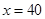 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?
(3)在(2)的条件下,他还清最后一笔贷款的那个月工资的余额是否能满足此月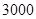 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: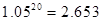 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com