Question

【题目】2013年1月，北京经历了59年来雾霾天气最多的一个月．据气象局统计，北京市2013年1月1日至1月30日这30天里有26天出现雾霾天气，《环境空气质量指数(AQI)技术规定(试行)》如表1：

表1　空气质量指数AQI分组表

AQI指数M	0～50	51～100	101～150	151～200	201～300	>300
级别	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ
状况	优	良	轻度污染	中度污染	重度污染	严重污染

表2是某气象观测点记录的连续4天里AQI指数M与当天的空气水平可见度y(km)的情况，表3是某气象观测点记录的北京市2013年1月1日至1月30日的AQI指数频数分布表．

表2　AQI指数M与当天的空气水平可见度y(km)的情况

AQI指数M	900	700	300	100
空气水平可见度y(km)	0.5	3.5	6.5	9.5

表3　北京市2013年1月1日至1月30日AQI指数频数分布表

AQI指数M	[0，200)	[200，400)	[400，600)	[600，800)	[800，1000]
频数	3	6	12	6	3

（1）设x＝，根据表2的数据，求出y关于x的线性回归方程．

(参考公式：，．)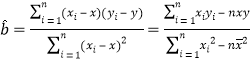

(2)小王在北京开了一家洗车店，经小王统计：当AQI指数低于200时，洗车店平均每天亏损约2000元；当AQI指数在200至400时，洗车店平均每天收入约4000元；当AQI指数不低于400时，洗车店平均每天收入约7000元．

①估计小王的洗车店在2013年1月份平均每天的收入；

②从AQI指数在[0，200)和[800，1000]内的这6天中抽取2天，求这2天的收入之和不低于5000元的概率．

Answer 1

【答案】（1）＝－x＋.（2）①5500元，②.

【解析】

（1）根据题中的数据及给出的公式求出和后可得回归方程．（2）①由题意可得在1月份30天中有3天洗车店每天亏损约2000元，有6天每天收入约4000元，有21天每天收入约7000元，然后求出平均数即为所求；②根据古典概型的概率和对立事件的概率求解．

(1)因为＝＝5，＝＝5,

＝92＋72＋32＋12＝140，

所以＝＝－，

故＝5－×5＝，

所以y关于x的线性回归方程是＝－x＋．

(2)①根据表3可知，在1月份30天中有3天洗车店每天亏损约2000元，有6天每天收入约4000元，有21天每天收入约7000元，

故1月份平均每天的收入约为×(－2000×3＋4000×6＋7000×21)＝5500(元)．

②记AQI指数在[0，200)内的3天为A1，A2，A3，AQI指数在[800，1000]内的3天为B1，B2，B3，则从[0，200)和[800，1000]内的这6天中抽取2天的所有情况有(A1，A2)，(A1，A3)，(A1，B1)，(A1，B2)，(A1，B3)，(A2，A3)，(A2，B1)，(A2，B2)，(A2，B3)，(A3，B1)，(A3，B2)，(A3，B3)，(B1，B2)，(B1，B3)，(B2，B3)，共15种，

其中满足这2天的收入之和低于5000元的情况有(A1，A2)，(A1，A3)，(A2，A3)，共3种，

故由古典概型的概率计算公式可得，这2天的收入之和低于5000元的概率为＝．

由对立事件的概率计算公式得，这2天的收入之和不低于5000元的概率为1－＝．