
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为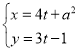 (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为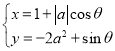 (
(![]() 为参数)
为参数)
(1)求![]() 和
和![]() 的普通方程;
的普通方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为其外接球球心,
为其外接球球心,![]() 与
与![]() ,
,![]() ,
,![]() 所成的角分别为
所成的角分别为![]() ,
,![]() ,
,![]() .有下列结论:
.有下列结论:
①该四面体的外接球的表面积为![]() ,
,
②该四面体的体积为10,
③![]()
④![]()
其中所有正确结论的编号为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三数学考试中,一般有一道选做题,学生可以从选修4-4和选修4-5中任选一题作答,满分10分.某高三年级共有1000名学生参加了某次数学考试,为了了解学生的作答情况,计划从该年级1000名考生成绩中随机抽取一个容量为10的样本,为此将1000名考生的成绩按照随机顺序依次编号为000~999.
(1)若采用系统抽样法抽样,从编号为000~999的成绩中随机确定的编号为026,求样本中的最大编号.
(2)若采用分层抽样法,按照学生选择选修4-4或选修4-5的情况将成绩分为两层,已知该校共有600名考生选择了选修4-4,400名考生选择了选修4-5,在选取的样本中,选择选修4-4的平均得分为6分,方差为2,选择选修4-5的平均得分为5分,方差为0.75.用样本估计该校1000名考生选做题的平均得分和得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过焦点且垂直于长轴的弦长为
,过焦点且垂直于长轴的弦长为![]() .
.
(1)已知点![]() 是椭圆上两点,点
是椭圆上两点,点![]() 为椭圆的上顶点,
为椭圆的上顶点,![]() 的重心恰好是椭圆的右焦点
的重心恰好是椭圆的右焦点![]() ,求
,求![]() 所
所
在直线的斜率;
(2)过椭圆的右焦点![]() 作直线
作直线![]() ,直线
,直线![]() 与椭圆分别交于点
与椭圆分别交于点![]() ,直线
,直线![]() 与椭圆分别交于点
与椭圆分别交于点![]() ,
,
且![]() ,求四边形
,求四边形![]() 的面积
的面积![]() 最小时直线
最小时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M是圆C:(x+1)2+y2=8上的动点,定点D(1,0),点P在直线DM上,点N在直线CM上,且满足![]() 2
2![]() ,
,![]()
![]() 0,动点N的轨迹为曲线E.
0,动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用黑白两种颜色随机地染如图所示表格中6个格子,每格子染一种颜色,并且从左往右数,不管数到哪个格子,总有黑色格子不少于白色格子的染色方法种数为________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com