
分析 根据基本不等式,可求出$\frac{x+1}{{x}^{2}-3x+3}$∈(0,$\frac{2\sqrt{7}+5}{3}$],解方程求出满足条件的x值,可得答案.
解答 解:∵x>-1,
∴$x+1+\frac{7}{x+1}$≥2$\sqrt{7}$,
∴$\frac{x+1}{{x}^{2}-3x+3}$=$\frac{1}{x+1+\frac{7}{x+1}-5}$∈(0,$\frac{2\sqrt{7}+5}{3}$],
若$\frac{x+1}{{x}^{2}-3x+3}$∈Z,
则$\frac{x+1}{{x}^{2}-3x+3}$=1,或$\frac{x+1}{{x}^{2}-3x+3}$=2,或$\frac{x+1}{{x}^{2}-3x+3}$=3,
解得:x=2-$\sqrt{2}$,或x=2+$\sqrt{2}$,或x=1,或x=$\frac{5}{2}$,或x=2,或x=$\frac{4}{3}$,
故M={2-$\sqrt{2}$,2+$\sqrt{2}$,1,$\frac{5}{2}$,2,$\frac{4}{3}$},
故答案为:{2-$\sqrt{2}$,2+$\sqrt{2}$,1,$\frac{5}{2}$,2,$\frac{4}{3}$}
点评 本题考查的知识点是集合表示法,基本不等式,是集合和不等式的综合应用,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,1)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
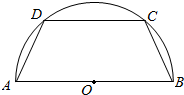 如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | y=log2(x-1) | C. | y=log2$\frac{1}{x}$ | D. | y=log2|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | $\frac{1}{10}$ | D. | -$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [e-3,e] | B. | (e-3,e) | C. | (-∞,e-3]∪[e,+∞) | D. | (0,e-3)∪(e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com