
如图,正三棱柱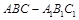 中,侧面
中,侧面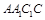 是边长为2的正方形,
是边长为2的正方形,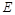 是
是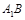 的中点,
的中点,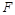 在棱
在棱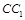 上.
上.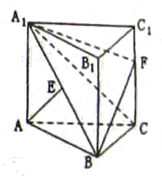
(1)当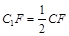 时,求三棱锥
时,求三棱锥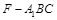 的体积.
的体积.
(2)当点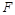 使得
使得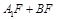 最小时,判断直线
最小时,判断直线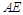 与
与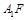 是否垂直,并证明结论.
是否垂直,并证明结论.
(1)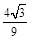 ,(2)垂直,利用线面垂直证明线线垂直
,(2)垂直,利用线面垂直证明线线垂直
解析试题分析:(1)因为侧面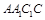 是边长为2的正方形,
是边长为2的正方形,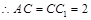
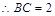
又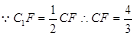
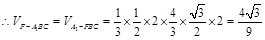
(2)解法1:将侧面 展开到侧面
展开到侧面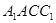 得到矩形
得到矩形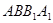 ,连结
,连结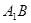 ,交
,交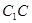 于点
于点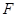 ,此时点
,此时点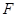 使得
使得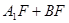 最小.此时
最小.此时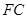 平行且等于
平行且等于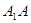 的一半,
的一半,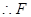 为
为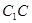 的中点.连接
的中点.连接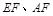
在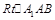 中,
中,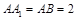 得
得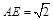
在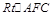 中,
中,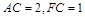 得
得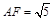
在等腰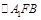 中,
中,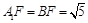 得
得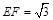
所以由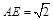 ,
,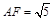 ,
,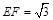 得
得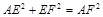 有勾股定理知
有勾股定理知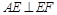
解法2:将侧面 展开到侧面
展开到侧面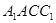 得到矩形
得到矩形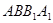 ,连结
,连结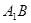 ,交
,交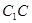 于点
于点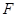 ,此时点
,此时点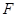 使得
使得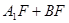 最小.此时
最小.此时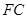 平行且等于
平行且等于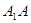 的一半,
的一半,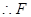 为
为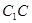 的中点.过点
的中点.过点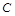 作
作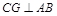 交
交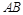 于
于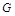 ,连接
,连接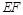 ,由
,由 且
且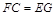 知四边形
知四边形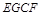 为
为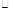 所以
所以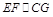 .在正三棱柱
.在正三棱柱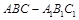 中知
中知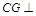 面
面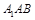 ,而
,而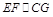 ,所以
,所以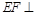 面
面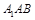 .
.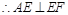
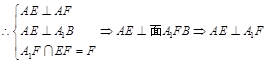
考点:本题考查了空间中的线面关系及体积的计算
点评:以棱锥为载体考查立体几何中的线面、面面、点面位置关系或体积是高考的亮点,掌握其判定性质及定理,是解决此类问题的关键


科目:高中数学 来源: 题型:解答题
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中,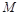 是
是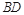 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.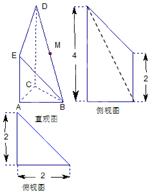
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求: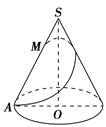
(1)设f(x)为绳子最短长度的平方,求f(x)表达式;
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com