
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,采集相应数据,对该公司2017年连续六个月的利润进行了统计,并绘制了相应的折线图,如图所示:
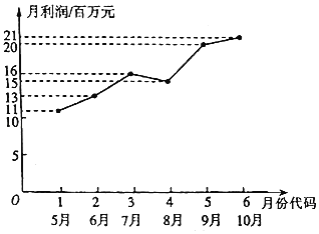
(1)折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2018年1月份的利润;
的线性回归方程,并预测该公司2018年1月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有采购成本分别为10万元![]() 包和12万元
包和12万元![]() 包的
包的![]() 、
、![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,不同类型的新型材料损坏的时间各不相同,已知生产新型材料的企业乙对
两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,不同类型的新型材料损坏的时间各不相同,已知生产新型材料的企业乙对![]() 、
、![]() 两种型号各100件新型材料进行过科学模拟测试,得到两种新型材料使用寿命频数统计如表:
两种型号各100件新型材料进行过科学模拟测试,得到两种新型材料使用寿命频数统计如表:
使用寿命 材料类型 | 1个月 | 2个月 | 3个月 | 4个月 | 总计 |
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
经甲公司测算,平均每包新型材料每月可以带来5万元收入,不考虑除采购成本之外的其他成本,假设每包新型材料的使用寿命都是整数月,且以频率作为每包新型材料使用寿命的概率,如果你是甲公司的负责人,以每包新型材料产生利润的期望值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程为![]() ,其中
,其中 .
.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m+2)![]() 是幂函数,设a=log54,b=
是幂函数,设a=log54,b=![]() ,c=0.5–0.2,则f(a),f(b),f(c)的大小关系是
,c=0.5–0.2,则f(a),f(b),f(c)的大小关系是
A.f(a)<f(b)<f(c)B.f(b)<f(c)<f(a)
C.f(c)<f(b)<f(a)D.f(c)<f(a)<f(b)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,
,![]() ,
,![]() 是其左右顶点,点
是其左右顶点,点![]() 是椭圆
是椭圆![]() 上任一点,且
上任一点,且![]() 的周长为6,若
的周长为6,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆![]() 于
于![]() ,
,![]() 两个不同点,证明:直线
两个不同点,证明:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新课程改革和高考综合改革的实施,高中教学以发展学生学科核心素养为导向,学习评价更关注学科核心素养的形成和发展.为此,我市于2018年举行第一届高中文科素养竞赛,竞赛结束后,为了评估我市高中学生的文科素养,从所有参赛学生中随机抽取1000名学生的成绩(单位:分)作为样本进行估计,将抽取的成绩整理后分成五组,从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
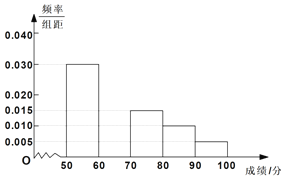
(1)请补全频率分布直方图并估计这1000名学生成绩的平均数(同一组数据用该组区间的中点值作代表);
(2)采用分层抽样的方法从这1000名学生的成绩中抽取容量为40的样本,再从该样本成绩不低于80分的学生中随机抽取2名进行问卷调查,求至少有一名学生成绩不低于90分的概率;
(3)我市决定对本次竞赛成绩排在前180名的学生给予表彰,授予“文科素养优秀标兵”称号.一名学生本次竞赛成绩为79分,请你判断该学生能否被授予“文科素养优秀标兵”称号.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四川省阆中中学某部根据运动场地的影响,但为尽大可能让学生都参与到运动会中来,在2018春季运动会中设置了五个项目,其中属于跑步类的两项,分别是200米和400米,另外三项分别为跳绳、跳远、跳高![]() 学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:
学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:

其中参加跑步类的人数所占频率为![]() ,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.
,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.
![]() 1
1![]() 求条形图中m和n的值以及抽取的13人中参加200米的学生人数;
求条形图中m和n的值以及抽取的13人中参加200米的学生人数;
![]() 2
2![]() 现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X,求离散型随机变量X的分布列与数学期望.
现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X,求离散型随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为![]() 的等边三角形
的等边三角形![]() 中,点
中,点![]() 分别是边
分别是边![]() 上的点,满足
上的点,满足![]() 且
且![]()
![]() ,将
,将![]() 沿直线
沿直线![]() 折到
折到![]() 的位置. 在翻折过程中,下列结论成立的是( )
的位置. 在翻折过程中,下列结论成立的是( )
A.在边![]() 上存在点
上存在点![]() ,使得在翻折过程中,满足
,使得在翻折过程中,满足![]() 平面
平面![]()
B.存在![]() ,使得在翻折过程中的某个位置,满足平面
,使得在翻折过程中的某个位置,满足平面![]() 平面
平面![]()
C.若![]() ,当二面角
,当二面角![]() 为直二面角时,
为直二面角时,![]()
D.在翻折过程中,四棱锥![]() 体积的最大值记为
体积的最大值记为![]() ,
,![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点F为抛物线的焦点,焦点F到直线3x-4y+3=0的距离为d1,焦点F到抛物线C的准线的距离为d2,且
,点F为抛物线的焦点,焦点F到直线3x-4y+3=0的距离为d1,焦点F到抛物线C的准线的距离为d2,且![]() 。
。
(1)抛物线C的标准方程;
(2)若在x轴上存在点M,过点M的直线l分别与抛物线C相交于P、Q两点,且![]() 为定值,求点M的坐标.
为定值,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com