
【题目】几位大学生响应国家的创业号召,开发了![]() 三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列
三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,试根据下列条件求出三款软件的激活码
,以此类推,试根据下列条件求出三款软件的激活码
(1)A款应用软件的激活码是该数列中第四个三位数的项数的平方
(2)B款应用软件的激活码是该数列中第一个四位数及其前所有项的和
(3)C款应用软件的激活码是满足如下条件的最小整数![]() :①
:①![]() ;②该数列的前
;②该数列的前![]() 项和为2的整数幂
项和为2的整数幂
【答案】(1)2809;(2)4083;(3)1897
【解析】
(1)讲数列按照规律重新书写成行列形式,依次观察三位数出现的顺序;
(2)根据第一问重新书写的形式找到第一个四位数1024所在位置即可求和;
(3)先确定第1000项出现在哪一行,再计算前m行所有项之和,要变成2的整数幂形式需要再加多少,即可求解.
(1)由题可以将数列排成如下形式:
1,
1,2,
1,2,4,
1,2,4,8,
1,2,4,8,16,
1,2,4,8,16,32,
…
由2的整数幂可知:第一个三位数是![]() ,
,
下一行产生第二个和第三个三位数,依次是![]() ,
,
下一行产生第四个三位数![]() ,
,
观察数列规律:①每行的行数即该行的项数,②第![]() 行的最后一项
行的最后一项![]() ,
,
第三个三位数![]() 出现在第9行最后一项,第四个三位数
出现在第9行最后一项,第四个三位数![]() 出现在第10行第8项,
出现在第10行第8项,
其项数为![]() ,
,![]()
所以A款应用软件的激活码是2809.
(2)由2的整数幂可知第一个四位数是![]() ,第11行第11项,根据规律:
,第11行第11项,根据规律:
设上面数列第![]() 行数列之和为
行数列之和为![]() ,可得
,可得![]() ,
,
所以第一个四位数及其以前所有项之和为
![]()
![]()
![]()
![]()
![]()
![]()
(3)由题:前![]() 行一共
行一共![]() 项,
项,
由条件①![]() ,设
,设![]() ,可得
,可得![]() ,
,
满足条件的最小整数![]() 至少在第45行或大于第45行中的某个项数,
至少在第45行或大于第45行中的某个项数,
根据条件②:前![]() 行所有项之和
行所有项之和
![]() ,
,
要满足这个数是2的整数幂,必须第![]() 行前
行前![]() 项之和为
项之和为![]() ,且
,且![]()
前![]() 项之和
项之和![]()
即![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
要使取值最小,只有当![]() 时满足题意,此时
时满足题意,此时![]() ,
,
![]()
所以满足条件的最小整数![]() .
.


科目:高中数学 来源: 题型:
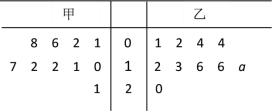
【题目】为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a表示.
(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值, 求图中a的所有可能取值;
(Ⅱ)将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设![]() ,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
(Ⅲ)记甲组阅读量的方差为![]() . 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为
. 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为![]() ;若A的阅读量为20,则记新甲组阅读量的方差为
;若A的阅读量为20,则记新甲组阅读量的方差为![]() ,试比较
,试比较![]() ,
,![]() ,
,![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海市旅游节刚落下帷幕,在旅游节期间,甲、乙、丙三位市民顾客分别获得一些景区门票的折扣消费券,数量如表1,已知这些景区原价和折扣价如表2(单位:元).
表1:
数量 | 景区1 | 景区2 | 景区3 |
甲 | 0 | 2 | 2 |
乙 | 3 | 0 | 1 |
丙 | 4 | 1 | 0 |
表2:
门票 | 景区1 | 景区2 | 景区3 |
原价 | 60 | 90 | 120 |
折扣后价 | 40 | 60 | 80 |
(1)按照上述表格的行列次序分别写出这三位市民获得的折扣消费券数量矩阵A和三个景区的门票折扣后价格矩阵B;
(2)利用你所学的矩阵知识,计算三位市民各获得多少元折扣?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的![]() 平面内,若函数
平面内,若函数![]() 的图象与
的图象与![]() 轴围成一个封闭的区域
轴围成一个封闭的区域![]() ,将区域
,将区域![]() 沿
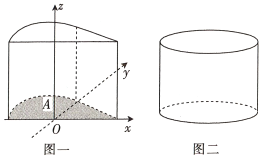
沿![]() 轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域![]() 的面积相等,则此圆柱的体积为__________.
的面积相等,则此圆柱的体积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 实数,函数
实数,函数![]() ,函数
,函数![]() .
.
(Ⅰ)令![]() ,当
,当![]() 时,试讨论函数
时,试讨论函数![]() 在其定义域内的单调性;
在其定义域内的单调性;
(Ⅱ)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com