
【题目】如图,在三棱锥P﹣ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB中点,PC=3PE.
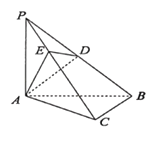
(1)求证:平面ADE⊥平面PBC;
(2)在AC上是否存在一点M,使得MB∥平面ADE?若存在,请确定点M的位置,并说明理由.
【答案】(1)证明见解析(2)存在,![]() 是
是![]() 中点;证明见解析
中点;证明见解析
【解析】
(1)根据已知可得![]() ,
,![]() ,可证BC⊥平面PAB,进而BC⊥AD,根据已知可得AD⊥PB,AD⊥平面PBC,即可证明结论;
,可证BC⊥平面PAB,进而BC⊥AD,根据已知可得AD⊥PB,AD⊥平面PBC,即可证明结论;
(2)存在M是AC中点时,MB∥平面ADE,取EC中点F,连结BM,MF,可证
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而证明平面
,进而证明平面![]() 平面
平面![]() ,即可证明结论.
,即可证明结论.
(1)证明:∵PA⊥平面ABC,![]() 平面ABC,∴BC⊥PA,
平面ABC,∴BC⊥PA,
![]() 平面PAB,
平面PAB,
∴BC⊥平面PAB,![]() 平面PAB,∴BC⊥AD,
平面PAB,∴BC⊥AD,
∵PA=AB,D为PB中点,∴AD⊥PB,
![]() 平面
平面![]() ,∴AD⊥平面PBC,
,∴AD⊥平面PBC,
∵AD平面ADE,∴平面ADE⊥平面PBC.
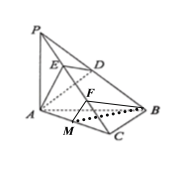
(2)点M是AC中点时,MB∥平面ADE,证明如下:
取EC中点F,连结BM,MF,
因为![]() 分别为
分别为![]() 的两个三等分点,
的两个三等分点,
在![]() 中,
中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】设椭圆方程![]() (
(![]() ),
),![]() ,
,![]() 是椭圆的左右焦点,以
是椭圆的左右焦点,以![]() ,
,![]() 及椭圆短轴的一个端点为顶点的三角形是面积为
及椭圆短轴的一个端点为顶点的三角形是面积为![]() 的正三角形.
的正三角形.
(1)求椭圆方程;
(2)过![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() ,设
,设![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 分别是线段
分别是线段![]() 的中点试,判断直线
的中点试,判断直线![]() 是否过定点?若过定点求出该定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的![]() ,对教师管理水平给出好评的学生人数为总数的
,对教师管理水平给出好评的学生人数为总数的![]() ,其中对教师教学水平和教师管理水平都给出好评的有120人.
,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的![]() 列联表:
列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
请问是否可以在犯错误概率不超过0.001的前提下,认为教师教学水平好评与教师管理水平好评有关?
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量![]() .
.
①求对教师教学水平和教师管理水平全好评的人数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() 千米,汽车从
千米,汽车从![]() 地匀速行驶到
地匀速行驶到![]() 地,速度不超过
地,速度不超过![]() 千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度
千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米小时)的函效:并求出当
(千米小时)的函效:并求出当![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,此时汽车的速度应调整为多大,才会使得运输成本最小,
,此时汽车的速度应调整为多大,才会使得运输成本最小,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棋盘上标有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子开始位于第
站,棋子开始位于第![]() 站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第
站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第![]() 站或第
站或第![]() 站时,游戏结束.设棋子位于第
站时,游戏结束.设棋子位于第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀硬币![]() 次后,求棋手所走步数之和
次后,求棋手所走步数之和![]() 的分布列与数学期望;
的分布列与数学期望;
(2)证明:![]() ;
;
(3)求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com