
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图象关于直线
,其图象关于直线![]() 对称.给出下面四个结论:①将
对称.给出下面四个结论:①将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数图象关于原点对称;②点
个单位长度后得到函数图象关于原点对称;②点![]() 为
为![]() 图象的一个对称中心;③
图象的一个对称中心;③![]() ;④
;④![]() 在区间
在区间![]() 上单调递增.其中正确的结论为( )
上单调递增.其中正确的结论为( )
A.①②B.②③C.②④D.①④
 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】百鸟蛋,又称九巧板,是类似于七巧板的益智拼图.相传是纪念哥伦布所制作的蛋形拼图,故又有哥伦布蛋形拼图一称.如图,九巧板由2个不规则四边形、2个大三角形、1个小三角形、2个不规则三角形和两个小扇形组成.在拼图时必须使用所有组件,角与边可相连接,但组件不能重叠.九巧板能拼摆出一百多种飞禽图形,可说是变化无穷、极富趣味,因此也被称为“百鸟朝凤”拼板.已知拼图中两个大三角形(图中阴影部分)为直角边长为2的等腰直角三角形,现用随机模拟的方法来估算此九巧板的总面积,随机在九巧板内选取100个点,发现有34个点落在两个大三角形内,则此九巧板的总面积约为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.

(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则以下说法错误的是( )
的中点,则以下说法错误的是( )
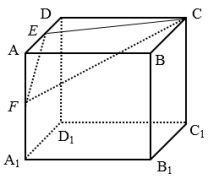
A.平面![]() 截正方体所的截面周长为
截正方体所的截面周长为![]()
B.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
C.三棱锥![]() 和
和![]() 体积相等
体积相等
D.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为A1、A2、…A10(如A2表示身高(单位:cm)在[150,155![]() 内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是


A.i<6B.i<7C.i<8D.i<9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com