
| A�� | 2 | B�� | $\frac{5}{2}$ | C�� | 3 | D�� | 5 |
���� $\overrightarrow{AC}$=��$\overrightarrow{AK}$⇒$\overrightarrow{AK}=\frac{1}{��}\overrightarrow{AC}=\frac{1}{��}��\overrightarrow{AB}+\overrightarrow{AD}��$=$\frac{1}{��}��2\overrightarrow{AE}+3\overrightarrow{AF}��=\frac{2}{��}\overrightarrow{AE}+\frac{3}{��}\overrightarrow{AF}$����E��F��K���㹲�߿ɵã�$\frac{2}{��}+\frac{3}{��}=1$���ɣ�
��� �⣺��$\overrightarrow{AB}$=2$\overrightarrow{AE}$��$\overrightarrow{AD}$=3$\overrightarrow{AF}$��
��$\overrightarrow{AC}$=��$\overrightarrow{AK}$��$\overrightarrow{AK}=\frac{1}{��}\overrightarrow{AC}=\frac{1}{��}��\overrightarrow{AB}+\overrightarrow{AD}��$=$\frac{1}{��}��2\overrightarrow{AE}+3\overrightarrow{AF}��=\frac{2}{��}\overrightarrow{AE}+\frac{3}{��}\overrightarrow{AF}$��
��E��F��K���㹲�߿ɵã�$\frac{2}{��}+\frac{3}{��}=1$���=5
��ѡ��D��
���� ������Ҫ�����������ӷ���ƽ���ı��η����Ӧ�ã��������߶�����Ӧ�ã����н���Ĺؼ���EFK���㹲�ߵ�ϵ��֮��Ϊ1�����ڻ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��N | B�� | M��∁UN | C�� | ∁UM��N | D�� | M��N |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
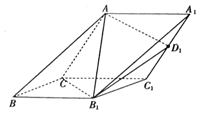 ��ͼ����������ABC-A1B1C1�У�����ACC1A1�����CBB1C1�������Σ���ACC1=��CC1B1=60�㣬AC=2$\sqrt{3}$��
��ͼ����������ABC-A1B1C1�У�����ACC1A1�����CBB1C1�������Σ���ACC1=��CC1B1=60�㣬AC=2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | -4 | C�� | ��4 | D�� | ��A�й� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com