
已知集合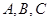 (不必相异)的并集
(不必相异)的并集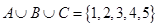 ,且
,且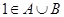
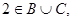
 ,则满足条件的有序三元组
,则满足条件的有序三元组 的个数是 个.
的个数是 个.
10584
【解析】
试题分析:本题画维恩图当然是可行的办法,但是在这种情况下,显得不那么直接和简便。为此可以先从题目中的各个元素入手,寻找解法。
如果把包含各个元素的情况计算出来,就得到了本题要的有序三元组的个数。
先考虑元素1,1在条件中和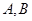 相关。把集合A是否包含元素1分成,2种情况,在集合B中也是同理。这样
相关。把集合A是否包含元素1分成,2种情况,在集合B中也是同理。这样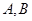 就有4种情况。而
就有4种情况。而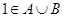 ,则A,B不能都不包含1。这时A,B对1共有3种情况。而在C中,仍然可以由是否包含1这2种情况。所以元素1的情况有6种。
,则A,B不能都不包含1。这时A,B对1共有3种情况。而在C中,仍然可以由是否包含1这2种情况。所以元素1的情况有6种。
同理,对元素2,3;同样是6种包含的情况。
再考虑元素4,4在三个集合中也可以分别分成是否包含2种情况,这样就有8种情况。再去除三个集合都不包含4的情况,这样4就有7种包含情况。
同理,对元素5,也有7种包含情况。
所以所求的有序三元组有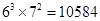 个。
个。
考点:集合的运算,集合的概念。
点评:难题,本题思路不易探寻得到。注意利用分类讨论思想,从题目中的各个元素入手,寻找得到解法。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com