
| 1 |
| 4 |
| 1 |
| 3 |
. |
| A |
. |
| A |
. |
| B |
. |
| A |
. |
| A |
. |
| B |
. |
| A |
. |
| A |
. |
| B |
|
| 5 |
| 8 |
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
| 21 |
| 8 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:不详 题型:解答题
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:北京期末题 题型:解答题
 ,乙每次投中的概率为
,乙每次投中的概率为 。
。查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市朝阳区高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 ,乙每次投中的概率为
,乙每次投中的概率为 求:
求:查看答案和解析>>
科目:高中数学 来源:北京市朝阳区08-09学年高二下学期期末考试(理) 题型:解答题
甲、乙两人玩投篮游戏,规则如下:
两人轮流投篮,每人至多投2次,甲先投,若有人投中则立即停止投篮,结束游戏,已知甲每次投中的概率为 ,乙每次投中的概率为
,乙每次投中的概率为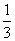 。
。
(I)求乙投篮次数不超过1次的概率;
(Ⅱ)甲、乙两人投篮次数的和为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com