
����Ŀ��ʹ��֧��������֧���Ѿ���Ϊ�������������Ҫ������֧����ʽ��ij����ͨ��ͳ�Ʒ���һ���ڳ���ÿ��ľ�����![]() (��Ԫ)��ÿ��ʹ��֧��������֧��������
(��Ԫ)��ÿ��ʹ��֧��������֧��������![]() (ǧ��)������ع�ϵ�����õ����һ��
(ǧ��)������ع�ϵ�����õ����һ��![]() ��7���������±�����������Ϊ��������.
��7���������±�����������Ϊ��������.
��һ | �ܶ� | ���� | ���� | ���� | ���� | ���� |
13 | 16 | 26 | 22 | 25 | 29 | 30 |
7 | 11 | 15 | 22 | 24 | 27 | 34 |
(��)����ɢ��ͼ���ж�![]() ��
��![]() ��һ���ʺ���Ϊÿ�쾻����Ļع鷽�����ͣ�������ع鷽��(
��һ���ʺ���Ϊÿ�쾻����Ļع鷽�����ͣ�������ع鷽��(![]() ��
��![]() ��
��![]() ��
��![]() ��ȷ��
��ȷ��![]() )��
)��

(��)����Ϊ�˴̼���һ���ѣ�������һ��չʹ��֧��������֧������齱����ܽ���7��Ԫ.�����г����飬�齱���ʹʹ��֧��������֧��������������6ǧ�ˣ�7ǧ�ˣ�8ǧ�ˣ�9ǧ�˵ĸ�������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .�Ծ��߳����Ƿ��б�Ҫ��չ�齱���
.�Ծ��߳����Ƿ��б�Ҫ��չ�齱���
�����: ![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��![]() ��
�� ��
��![]() .
.
���𰸡�(��) ��������(��) �����б�Ҫ��չ�齱�
��������
(��)������������ϵ�У�����ɢ��ͼ�����Է���ѡ��![]() ��Ϊÿ�쾻����Ļع鷽�����ͱȽϺ��ʣ������
��Ϊÿ�쾻����Ļع鷽�����ͱȽϺ��ʣ������![]() �����������Ĺ�ʽ�������
�����������Ĺ�ʽ�������![]() ���������ع鷽�̣�
���������ع鷽�̣�
(��)������ɢ������ֲ��е����ʣ��������![]() ֵ��Ȼ����������ѧ������������(��)
ֵ��Ȼ����������ѧ������������(��)
����Ļع�ֱ�߷��̣�����Ԥ�����������ȥ�ܽ��𣬿���������еľ���������жϳ��Ƿ��б�Ҫ��չ�齱�.
��:(��)ɢ��ͼ��ͼ��ʾ
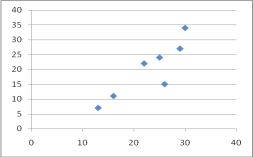
����ɢ��ͼ���жϣ�ѡ��![]() ��Ϊÿ�쾻����Ļع鷽�����ͱȽϺ���
��Ϊÿ�쾻����Ļع鷽�����ͱȽϺ���
![]() ��
��![]()
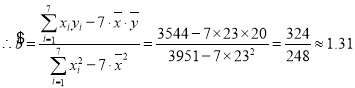
![]()
![]()
![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]()
(��)![]() ��
��![]()
![]() ���չ��ʹ��֧��������֧��������
���չ��ʹ��֧��������֧��������![]() ������Ϊ
������Ϊ
![]() (ǧ��)
(ǧ��)
��(��)�ã���![]() ʱ��
ʱ��![]()
��ʱ���еľ�����ԼΪ![]() ���ʳ����б�Ҫ��չ�齱�
���ʳ����б�Ҫ��չ�齱�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ��
��
��1��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() û�н��㣬��
û�н��㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ��������
��������![]() ��
��![]() ��ͼ������ֻ��һ�������㣬��ʵ��
��ͼ������ֻ��һ�������㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����1̨���������ֻ���ʹ���������̭.�ڹ�������ʱ������һ���Զ����ά����ÿ��ά�������200Ԫ������ʵ��ά��һ�λ�����ά����Ա֧��С�ѣ�С��ÿ��50Ԫ.�ڻ���ʹ���ڼ䣬���ά������������ʱ�����ά�����������ÿά��һ����֧��ά�������500Ԫ������֧��С��.��������ڹ������ʱӦͬʱһ���Թ���ά����Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڵ�ά������������ͳ�Ʊ���
���� | 8 | 9 | 10 | 11 | 12 |
Ƶ�� | 10 | 20 | 30 | 30 | 10 |
��x��ʾ1̨����������ʹ�����ڵ�ά������y��ʾ1̨������ά��������ķ��ã���λ��Ԫ����![]() ��ʾ������ͬʱ�����ά�������.
��ʾ������ͬʱ�����ά�������.
��1����![]() =10����y��x�ĺ�������ʽ��
=10����y��x�ĺ�������ʽ��
��2����Ҫ��ά����������![]() ����Ƶ�ʲ�С��0.8����n����Сֵ��
����Ƶ�ʲ�С��0.8����n����Сֵ��
��3��������100̨�����ڹ�����ͬʱÿ̨������10��ά����ÿ̨������11��ά���ֱ������100̨������ά����������õ�ƽ�������Դ���Ϊ�������ݣ�����1̨������ͬʱӦ����10�λ���11��ά����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱߡ�ABC�У�AC��4��D�DZ�AC�ϵĵ㣨����A��C�غϣ�������D��DE��BC��AB�ڵ�E����DE����ADE��������ʹ��ƽ��ADE��ƽ��BCDE����ͼ2��ʾ��
��1��������ֱ��BE��AC��ֱ��ȷ��ͼ1�е�D��λ�ã�
��2��֤�������۵�D��λ����Σ������D��AE��B������ֵ��Ϊ��ֵ������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ö�ʵؾ��ȵ�Ӳ�ң����¼�A=����һöӲ�����泯�������¼�B=���ڶ�öӲ�ҷ��泯����.
��1��д�������ռ䣬���о�A��B�����������㣻
��2�����н�������ȷ���ǣ� ��.
A.A��B��Ϊ�����¼� B.A��B���� C.A��B��� D.P��A��=P��B��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж�����˵���Ƿ���ȷ����������ٳ�����
��1��������¼�һ���Ƕ����¼��������¼���һ���ǻ����¼���
��2��������¼���һ���Ƕ����¼��������¼�һ���ǻ����¼���
��3���¼�![]() ���¼�B��������һ�������ĸ���һ����
���¼�B��������һ�������ĸ���һ����![]() ��B��ǡ��һ�������ĸ��ʴ�
��B��ǡ��һ�������ĸ��ʴ�
��4���¼�![]() ���¼�Bͬʱ�����ĸ���һ����
���¼�Bͬʱ�����ĸ���һ����![]() ��B��ǡ��һ�������ĸ���С.
��B��ǡ��һ�������ĸ���С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ���Ҵ���ʵ����
���Ҵ���ʵ����![]() ��ʹ�ö��ڶ�����������
��ʹ�ö��ڶ�����������![]() ������
������![]() ��������ƴ˺���
��������ƴ˺���![]() ���С�����
��������![]() ��.
��.
��1���жϺ���![]() �Ƿ���С�
�Ƿ���С�![]() ���ʡ��������С�
���ʡ��������С�![]() ���ʡ����������
���ʡ����������![]() ��ֵ�ļ��ϣ��������С�
��ֵ�ļ��ϣ��������С�![]() ���ʡ�����˵�����ɣ�
���ʡ�����˵�����ɣ�
��2����֪����![]() ���С�
���С�![]() ���ʡ����ҵ�
���ʡ����ҵ�![]() ʱ��
ʱ��![]() ������
������![]() ������
������![]() �ϵ�ֵ��
�ϵ�ֵ��
��3����֪����![]() �Ⱦ��С�
�Ⱦ��С�![]() ���ʡ����־��С�
���ʡ����־��С�![]() ���ʡ����ҵ�
���ʡ����ҵ�![]() ʱ��
ʱ��![]() ��������
��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��2017�������㣬��ʵ��
��2017�������㣬��ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̹�������֮����һ�����͵ij��з�ʽ------������������Ҳ��ʼ����Ϲ����ʮ����г��У�һ��С�һ���ó����Ĺ��������ڹ����ṩ�ij����ǡ�����eQ����ÿ����շѰ���ʻ��̼��ó�ʱ��,���ǡ�1Ԫ/����+0.1Ԫ/���ӡ��������������ϰ�ص�10���ÿ�����ù����������°࣬���ڶ³����أ�ÿ��·�Ͽ������ѵ�ʱ����һ���������������һ��ʱ��ͳ��40��·�Ͽ�������ʱ���ڸ�ʱ����ڵ�������£�
ʱ�䣨���ӣ� |
|
|
|
|
|
���� | 8 | 14 | 8 | 8 | 2 |
�Ը�ʱ��η�����Ƶ����Ϊ���ʣ�����ÿ��·�Ͽ������ѵ�ʱ����Ϊ�ó�ʱ�䣬��ΧΪ![]() ����.
����.
��������������.�°�ʱ����һ�ι�������·�Ͽ���������45���ӣ��������п�ѡ��Ľ�ͨ�����е�һ������ѡ����![]() ��4��ʹ�ù�������������ѡ��Ĵ�������
��4��ʹ�ù�������������ѡ��Ĵ�������![]() �ķֲ��к�����.
�ķֲ��к�����.
������������ÿ�����°�ʹ�ù�������2�Σ�һ���£���20����㣩ƽ���ó����ô�Լ�Ƕ��٣�ͬһʱ�Σ��ø�������е�ֵ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ����Բ�����һ���˵����������㹹�ɵ������ε����Ϊ
����Բ�����һ���˵����������㹹�ɵ������ε����Ϊ![]() .
.
��1������Բ![]() �ķ���ʽ��
�ķ���ʽ��
��2����֪��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ����.
����.
�����߶�![]() �е�ĺ�����Ϊ
�е�ĺ�����Ϊ![]() ����б��
����б��![]() ��ֵ��
��ֵ��
����֪��![]() ����֤��
����֤�� ![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com