
【题目】设函数f(x)=asin(2x+ ![]() )+b
)+b
(1)若a>0,求f(x)的单调递增区间;
(2)当x∈[0, ![]() ]时,f(x)的值域为[1,3],求a,b的值.
]时,f(x)的值域为[1,3],求a,b的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,点P(0,﹣1)是椭圆C1: ![]() =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D. 
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足2a1+a3=3a2 , 且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=an+log2 ![]() ,Sn=b1+b2+…bn , 求使 Sn﹣2n+1+47<0 成立的正整数n的最小值.
,Sn=b1+b2+…bn , 求使 Sn﹣2n+1+47<0 成立的正整数n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的![]() 分别为14,18,则输出的
分别为14,18,则输出的![]() 为( )
为( )
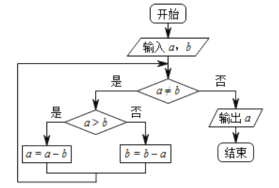
A. 0 B. 2 C. 4 D. 14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,85],得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产A、B、C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足不等式|x﹣A|<B(A∈R,B>0)的实数x的集合叫做A的B 邻域.若a+b﹣t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com