
【题目】已知函数![]()
(I)求函数f(x)的最小正周期和对称中心的坐标
(II)设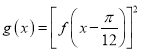 ,求函数g(x)在
,求函数g(x)在![]() 上的最大值,并确定此时x的值
上的最大值,并确定此时x的值
【答案】(I) ![]() ,
, ![]() . (II) 见解析.
. (II) 见解析.
【解析】试题分析:(Ⅰ)由二倍角公式和化一公式化简可得![]() ;
;
(Ⅱ)由(Ⅰ)知![]() 的解析式,把
的解析式,把![]() 代入求
代入求![]() ,进而求出g(x),结合x的范围,求出最大值即可.
,进而求出g(x),结合x的范围,求出最大值即可.
试题解析:(I) ![]()
![]()
![]()
![]()
∴函数f(x)的最小正周期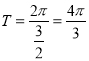 ,
,
由![]() ,得
,得![]() ,
,
∴函数f(x)的对称中心的坐标为![]() .
.
(II)由(I)可得f(x-![]() )=2sin[
)=2sin[![]() (x-
(x-![]() )+
)+![]() ]=2sin(
]=2sin(![]() x+
x+![]() ),
),
∴g(x)=[f(x-![]() )]2=4×
)]2=4×![]() =2-2cos(3x+
=2-2cos(3x+![]() ),
),
∵x∈[-![]() ,
,![]() ],∴-
],∴-![]() ≤3x+
≤3x+![]() ≤
≤![]() ,
,
∴当3x+![]() =π,即x=
=π,即x=![]() 时,g(x)max=4.
时,g(x)max=4.
点睛:三角函数式的化简要遵循“三看”原则:(1)一看“角”,这是最重要的一环,通过看角之间的区别和联系,把角进行合理的拆分,从而正确使用公式;(2)而看“函数名称”看函数名称之间的差异,从而确定使用公式,常见的有“切化弦”;(3)三看“结构特征”,分析结构特征,可以帮助我们找到变形的方向,如“遇到分式通分”等.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前9项和为63.
,其前9项和为63.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若对任意正整数n,都有
,若对任意正整数n,都有![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员的5次测试成绩如下图所示:
甲 | 茎 | 乙 |
5 7 | 1 | 6 8 |
8 8 2 | 2 | 3 6 7 |
设s1 , s2分别表示甲、乙两名运动员测试成绩的标准差, ![]() 分别表示甲、乙两名运动员测试成绩的平均数,则有( )
分别表示甲、乙两名运动员测试成绩的平均数,则有( )
A.![]() ,s1<s2
,s1<s2
B.![]() ,s1>s2
,s1>s2
C.![]() ,s1>s2
,s1>s2
D.![]() ,s1=s2
,s1=s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A′B′C′D′中,AB=2 ![]() ,AD=2
,AD=2 ![]() ,AA′=2,
,AA′=2,
(Ⅰ)求异面直线BC′ 和AD所成的角;
(Ⅱ)求证:直线BC′∥平面ADD′A′.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面是边长为2的菱形,且∠BAD= ![]() ,AA1⊥平面ABCD,AA1=1,设E为CD中点
,AA1⊥平面ABCD,AA1=1,设E为CD中点 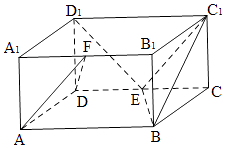
(1)求证:D1E⊥平面BEC1
(2)点F在线段A1B1上,且AF∥平面BEC1 , 求平面ADF和平面BEC1所成锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系![]() 的坐标平面
的坐标平面![]() 内,若函数
内,若函数 的图象与
的图象与![]() 轴围成一个封闭区域
轴围成一个封闭区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域![]() 面积相等,则此圆柱的体积为__________.
面积相等,则此圆柱的体积为__________.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱![]() 容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面
容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面![]() 水平放置,如图所示,点
水平放置,如图所示,点![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 上,水面恰好过点
上,水面恰好过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)证明: ![]() ;
;
(2)若底面![]() 水平放置时,求水面的高.
水平放置时,求水面的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com