
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,若c=2![]() ,sinB=2sinA.
,sinB=2sinA.
(1)若C=![]() ,求a,b的值;
,求a,b的值;
(2)若cosC=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6名奥运会志愿者,其中志愿者![]() 通晓日语,
通晓日语, ![]() 通晓俄语,
通晓俄语, ![]() 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求![]() 被选中的概率;
被选中的概率;
(2)求![]() 和
和![]() 不全被选中的概率;
不全被选中的概率;
(3)若6名奥运会志愿者每小时派两人值班,现有两名只会日语的运动员到来,求恰好遇到![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 外的有一点
外的有一点![]() ,过点
,过点![]() 作直线
作直线![]() .
.
(1)当直线![]() 过圆心
过圆心![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(3)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求直线
时,求直线![]() 被圆
被圆![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上的一动点,过点
上的一动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)当切线![]() 的长度为
的长度为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2) 若![]() 的外接圆为圆
的外接圆为圆![]() ,试问:当
,试问:当![]() 在直线
在直线![]() 上运动时,圆
上运动时,圆![]() 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体;第二次切削沿长方体的对角面刨开,得到两个三棱柱;第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
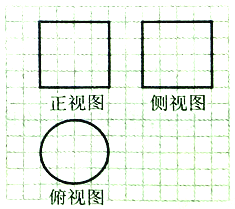
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com