
【题目】在极坐标系中,曲线C1:ρ=2cosθ,曲线C2:ρ=(ρcosθ+4)cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C的参数方程为  (t为参数). (Ⅰ)求C1 , C2的直角坐标方程;
(t为参数). (Ⅰ)求C1 , C2的直角坐标方程;
(Ⅱ)C与C1 , C2交于不同四点,这四点在C上的排列顺次为H,I,J,K,求||HI|﹣|JK||的值.
【答案】解:(Ⅰ)∵曲线C1:ρ=2cosθ,∴ρ2=2ρcosθ, ∵ρ2=x2+y2 , x=ρcosθ,y=ρsinθ,
∴曲线C1的直角坐标方程为(x﹣1)2+y2=1.
∵曲线C2:ρ=(ρcosθ+4)cosθ.
∴ρ2sin2θ=4ρcosθ,
∴曲线C2的直角坐标方程为y2=4x.
(Ⅱ)不妨设四点在C上的排列顺次至上而下为H,I,J,K,
它们对应的参数分别为t1 , t2 , t3 , t4 , 如图,连结C1 , J,
则△C1IJ为正三角形,
∴|IJ|=1,||HI|﹣|JK||=||HI|﹣|IK|+|IJ||=||t1|﹣|t4|+1|=|﹣(t1+t4)+1|,
把曲线C的参数方程为 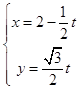 (t为参数)代入y2=4x,
(t为参数)代入y2=4x,
得: ![]() ,即3t2+8t﹣32=0,故
,即3t2+8t﹣32=0,故 ![]() ,
,
∴||HI|﹣|JK||= ![]() .
.
【解析】(Ⅰ)由ρ2=x2+y2 , x=ρcosθ,y=ρsinθ,能求出C1 , C2的直角坐标方程.(Ⅱ)设四点在C上的排列顺次至上而下为H,I,J,K,它们对应的参数分别为t1 , t2 , t3 , t4 , 连结C1 , J,则△C1IJ为正三角形,||HI|﹣|JK||=||HI|﹣|IK|+|IJ||=||t1|﹣|t4|+1|=|﹣(t1+t4)+1|,把曲线C的参数方程代入y2=4x,得3t2+8t﹣32=0,由此能求出||HI|﹣|JK||的值.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx﹣3x2﹣11x.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)≤(a﹣3)x2+(2a﹣13)x+1恒成立,求整数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1F2 , 这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,记椭圆与双曲线的离心率分别为e1 , e2 , 则e1e2的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.( ![]() ,+∞)
,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4 ![]() ,∠ABC=30°.
,∠ABC=30°. 
(I)求证:AC⊥BD;
(II)若二面角B﹣AC﹣D为45°,求直线AB与平面ACD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知2sin2A+sin(A﹣B)=sinC,且 ![]() . (Ⅰ)求
. (Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)若c=2, ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则至少有两个数位于同行或同列的概率是( ) 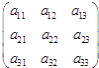
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100] 
(1)求频率分布直方图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60)的受访职工中,随机抽取2人,求此2人的评分恰好有一人在[40,50)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x﹣a|,a∈R.
(1)当a=1时,求不等式f(x)+|2x﹣5|≥6的解集;
(2)若函数g(x)=f(x)﹣|x﹣3|的值域为A,且[﹣1,2]A,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行“庆元旦”教工羽毛球单循环比赛(任意两个参赛队只比赛一场),共有高一、高二、高三三个队参赛,高一胜高二的概率为 ![]() ,高一胜高三的概率为
,高一胜高三的概率为 ![]() ,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
(Ⅰ)若高三获得冠军概率为 ![]() ,求P.
,求P.
(Ⅱ)记高三的得分为X,求X的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com