
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.如图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”. 
(1)求m,n的值,并求这100名学生月消费金额的样本平均数 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】按照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为 ![]() ;如果他买进该产品的单价为n元,则他的满意度为
;如果他买进该产品的单价为n元,则他的满意度为 ![]() .如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2 , 则他对这两种交易的综合满意度为
.如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2 , 则他对这两种交易的综合满意度为 ![]() .现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mAm元和mB元,甲买进A与卖出B的综合满意度为h甲 , 乙卖出A与买进B的综合满意度为h乙 .
.现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mAm元和mB元,甲买进A与卖出B的综合满意度为h甲 , 乙卖出A与买进B的综合满意度为h乙 .
(1)求h甲和h乙关于mA、mB的表达式;当mA= ![]() mB时,求证:h甲=h乙;
mB时,求证:h甲=h乙;
(2)设mA= ![]() mB , 当mA、mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
mB , 当mA、mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=log2(2x+a)的定义域为(0,+∞).
(1)求a的值;
(2)若g(x)=log2(2x+1),且关于x的方程f(x)=m+g(x)在[1,2]上有解,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=﹣x与直线y=k(x+1)(k≠0)相交于A、B两点,O是坐标原点.
(1)当k= ![]() 时,求|AB|的长;
时,求|AB|的长;
(2)求证无论k为何值都有OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
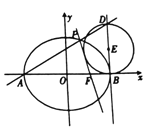
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|loga|x﹣1||(a>0,a≠1),若x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则 ![]() +
+ ![]() +
+ ![]() +
+ ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b. 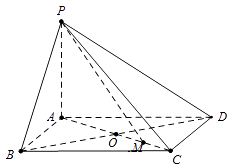
(1)求证:平面PBD⊥平面PAC;
(2)设AC与BD交于点O,M为OC中点,若二面角O﹣PM﹣D的正切值为2 ![]() ,求a:b的值.
,求a:b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数.
上是增函数.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com