
在 中,角
中,角 ,
, ,
,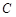 所对的边分别是
所对的边分别是 ,
,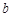 ,
,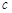 ,已知
,已知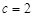 ,
,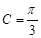 .
.
(1)若 的面积等于
的面积等于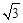 ,求
,求 ,
,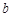 ;
;
(2)若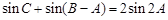 ,求
,求 的面积.
的面积.
(1)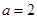 ,
, ;(2)
;(2)
解析试题分析:(1)利用余弦定理 及面积公式
及面积公式 ,列方程组就可求出
,列方程组就可求出 ,
,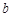 ;(2)要求三角形面积,关键在于求出边长.但已知等式条件不能直接利用正余弦定理将角化为边,所以先根据诱导公式将
;(2)要求三角形面积,关键在于求出边长.但已知等式条件不能直接利用正余弦定理将角化为边,所以先根据诱导公式将 化为
化为 再利用两角和与差的正弦公式及二倍角公式化简,得
再利用两角和与差的正弦公式及二倍角公式化简,得 ,此时约分时注意讨论零的情况.当
,此时约分时注意讨论零的情况.当 时,
时, ,
, ;当
;当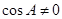 时,得
时,得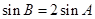 ,对这一式子有两个思路,一是用正弦定理化边,二是继续化角,
,对这一式子有两个思路,一是用正弦定理化边,二是继续化角,
试题解析:(1)由余弦定理及已知条件得, , 2分
, 2分
又因为 的面积等于
的面积等于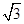 ,所以
,所以 ,得
,得 . 4分
. 4分
联立方程组 解得
解得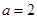 ,
, . 7分
. 7分
(2)由题意得 ,即
,即 ,
,
当 时,
时, ,
, ,
, ,
, , 10分
, 10分
当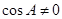 时,得
时,得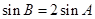 ,由正弦定理得
,由正弦定理得 ,
,
联立方程组 解得
解得 ,
, . 13分
. 13分
所以 的面积
的面积 . 14分
. 14分
考点:正余弦定理,面积公式.


科目:高中数学 来源: 题型:解答题
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2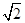 ,点M在线段PQ上.
,点M在线段PQ上.
(1)若OM= ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,甲船以每小时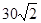 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距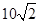 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com