
为加快旅游业的发展,新余市2013年面向国内发行总量为200万张的“仙女湖之旅”优惠卡,向省外人士发行的是金卡,向省内人士发行的是银卡.某旅游公司组织了一个有36名游客的旅游团到新余仙女湖旅游,其中 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(2)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等概率.
(1)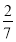 ;(2)
;(2)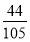 .
.
【解析】
试题分析:(1)根据题意,36人的旅游团中持金卡的人数为: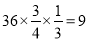 ,
,
持银卡的人数为: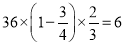 ,可用古典概型求在该团中随机采访2名游客,求恰有1人持银卡的概率;
,可用古典概型求在该团中随机采访2名游客,求恰有1人持银卡的概率;
(2)事件“在该团中随机采访2名游客,求其中持金卡与持银卡人数相等”可看作两个互斥事件的和事件, 即:“在该团中随机采访2名游客,所抽中的两人都不持有优惠卡”与“在该团中随机采访2名游客,所抽中的两个人中一人持有金卡,另一人持有银卡”,再用古典概型求这两个事件的概率即可.
试题解析:(1)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.
设事件A为“采访该团2人,恰有1人持银卡”, 1分
则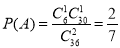
所以采访该团2人,恰有1人持银卡的概率是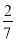 . 6分
. 6分
(2)设事件B为“采访该团2人,持金卡人数与持银卡人数相等”,可以分为:
事件B1为“采访该团2人,持金卡0人,持银卡0人”,或事件B2为“采访该团2人,持金卡1人,持银卡1人”两种情况,则
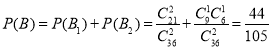
所以采访该团2人,持金卡与持银卡人数相等的概率是 . 12分
. 12分
考点:1、古典概型;2、互斥事件的和事件.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源:2015届江西赣州六校高二上学期期末联考理科数学试卷(解析版) 题型:选择题
设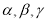 为两两不重合的平面,
为两两不重合的平面,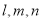 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
(1)若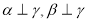 ,则
,则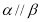 ;
;
(2)若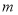
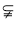
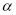 ,
,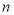
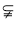
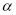 ,
,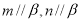 ,则
,则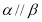 ;
;
(3)若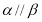 ,
,
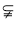
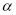 ,则
,则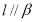 ;
;
(4)若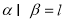 ,
, ,
,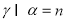 ,
,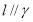 ,则
,则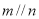 .
.
其中正确的命题是( )
A、(1)(3) B、(2)(3)
C、(2)(4) D、(3)(4)
查看答案和解析>>
科目:高中数学 来源:2015届江西新余市高二上学期期末理科A数学试卷(解析版) 题型:选择题
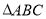 中,
中,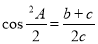 ,则
,则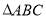 形状是( )
形状是( )
A. 正三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com