
【题目】设整数集合![]() ,其中
,其中![]() ,且对于任意
,且对于任意![]() ,若
,若![]() ,则
,则![]()
(1)请写出一个满足条件的集合![]() ;
;
(2)证明:任意![]() ;
;
(3)若![]() ,求满足条件的集合
,求满足条件的集合![]() 的个数.
的个数.
【答案】(1)![]() (2)证明见解析 (3)16个
(2)证明见解析 (3)16个
【解析】
(1)根据题目条件,令![]() ,即可写出一个集合
,即可写出一个集合![]() ;
;
(2)由反证法即可证明;
(3)因为任意的![]() ,所以集合
,所以集合![]() 中至多5个元素.设
中至多5个元素.设![]() ,先通过判断集合
,先通过判断集合![]() 中前
中前![]() 个元素的最大值可以推出
个元素的最大值可以推出![]() ,故集合
,故集合![]() 的个数与集合
的个数与集合![]() 的子集个数相同,即可求出.
的子集个数相同,即可求出.
(1)答案不唯一. 如![]() ;
;
(2)假设存在一个![]() 使得
使得![]() ,
,
令![]() ,其中
,其中![]() 且
且![]() ,
,
由题意,得![]() ,
,
由![]() 为正整数,得
为正整数,得![]() ,这与
,这与![]() 为集合
为集合![]() 中的最大元素矛盾,
中的最大元素矛盾,
所以任意![]() ,
,![]() .
.
(3)设集合![]() 中有
中有![]() 个元素,
个元素,![]() ,
,
由题意,得![]() ,
,![]() ,
,
由(2)知,![]() .
.
假设![]() ,则
,则![]() .
.
因为![]() ,
,
由题设条件,得![]() ,
,
因为![]() ,
,
所以由(2)可得![]() ,
,
这与![]() 为
为![]() 中不超过
中不超过![]() 的最大元素矛盾,
的最大元素矛盾,
所以![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() .
.
任给集合![]() 的
的![]() 元子集
元子集![]() ,令
,令![]() ,
,
以下证明集合![]() 符合题意:
符合题意:
对于任意![]()
![]() ,则
,则![]() .
.
若![]() ,则有
,则有![]() ,
,
所以![]() ,
,![]() ,从而
,从而![]() .
.
故集合![]() 符合题意,
符合题意,
所以满足条件的集合![]() 的个数与集合
的个数与集合![]() 的子集个数相同,
的子集个数相同,
故满足条件的集合![]() 有
有![]() 个.
个.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义:对于任意![]() ,满足条件
,满足条件![]() 且
且![]() (M是与n无关的常数)的无穷数列
(M是与n无关的常数)的无穷数列![]() 称为M数列.
称为M数列.
(1)若等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,判断数列
,判断数列![]() 是否是M数列,并说明理由;
是否是M数列,并说明理由;
(2)若各项为正数的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,证明:数列
,证明:数列![]() 是M数列,并指出M的取值范围;
是M数列,并指出M的取值范围;
(3)设数列![]() ,问数列
,问数列![]() 是否是M数列?请说明理由.
是否是M数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商贸公司售卖某种水果.经市场调研可知:在未来![]() 天内,这种水果每箱的销售利润
天内,这种水果每箱的销售利润![]() (单位:元)与时间
(单位:元)与时间![]() ,单位:天)之间的函数关系式为
,单位:天)之间的函数关系式为![]() , 且日销售量
, 且日销售量![]() (单位:箱)与时间
(单位:箱)与时间![]() 之间的函数关系式为
之间的函数关系式为![]()
①第![]() 天的销售利润为__________元;
天的销售利润为__________元;
②在未来的这![]() 天中,公司决定每销售
天中,公司决定每销售![]() 箱该水果就捐赠
箱该水果就捐赠![]() 元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间
元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间![]() 的增大而增大,则
的增大而增大,则![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①若函数f(x)既是奇函数又是偶函数,则f(x)的值域为{0};
②若函数f(x)是偶函数,则f(|x|)=f(x);
③若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数;
④若函数f(x)存在反函数f﹣1(x),且f﹣1(x)与f(x)不完全相同,则f(x)与f﹣1(x)图象的公共点必在直线y=x上;
其中真命题的序号是 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
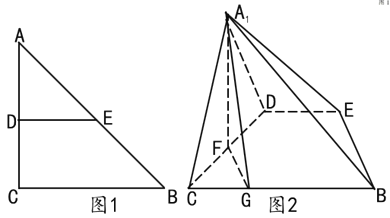
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com