
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:不详 题型:解答题
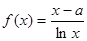 ,其中
,其中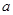 为实数.
为实数.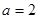 时,求曲线
时,求曲线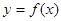 在点
在点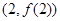 处的切线方程;
处的切线方程;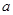 ,使得对任意
,使得对任意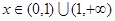 ,
,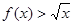 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出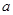 的值并加以证明.
的值并加以证明.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
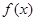 在
在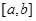 上连续,在
上连续,在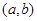 内可导,且
内可导,且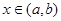 时,
时,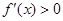 ,又
,又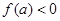 ,则 ( )
,则 ( )A.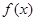 在 在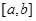 上单调递增,且 上单调递增,且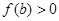 |
B.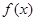 在 在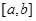 上单调递增,且 上单调递增,且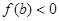 |
C.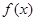 在 在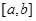 上单调递减,且 上单调递减,且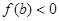 |
D.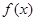 在 在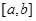 上单调递增,但 上单调递增,但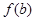 的符号无法判断 的符号无法判断 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
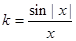 (k>0)有且仅有两个不同的零点
(k>0)有且仅有两个不同的零点 ,
,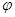 (
( >
>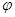 ),则以下有关两零点关系的结论正确的是
),则以下有关两零点关系的结论正确的是A.sin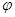 = =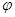 cos cos | B.sin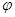 =- =-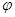 cos cos |
C.sin = = cos cos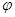 | D.sin =- =- cos cos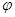 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com