
ЁОЬтФПЁПвбжЊУќЬт![]() ЃКШє
ЃКШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
ЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A. УќЬт![]() ЕФЗёУќЬтЪЧЁАШє
ЕФЗёУќЬтЪЧЁАШє![]() ЃЌдђ
ЃЌдђ![]() ЁБ
ЁБ
B. УќЬт![]() ЕФФцЗёУќЬтЪЧЁАШє
ЕФФцЗёУќЬтЪЧЁАШє![]() ЃЌдђ
ЃЌдђ![]() ЁБ
ЁБ
C. УќЬт![]() ЪЧецУќЬт
ЪЧецУќЬт
D. УќЬт![]() ЕФФцУќЬтЪЧецУќЬт
ЕФФцУќЬтЪЧецУќЬт
ЁОД№АИЁПD
ЁОНтЮіЁПA. УќЬт![]() ЕФЗёУќЬтЪЧШє
ЕФЗёУќЬтЪЧШє![]()
B. УќЬт![]() ЕФФцЗёУќЬтЪЧЁАШє
ЕФФцЗёУќЬтЪЧЁАШє![]() ЃЌдђ
ЃЌдђ![]()
![]()
C. УќЬт![]() ЪЧМйУќЬтЃЌБШШчЕБx=-3,ОЭВЛТњзуЬѕМўЃЌЙЪбЁЯюВЛе§ШЗ.
ЪЧМйУќЬтЃЌБШШчЕБx=-3,ОЭВЛТњзуЬѕМўЃЌЙЪбЁЯюВЛе§ШЗ.
D. УќЬт![]() ЕФФцУќЬтЪЧШє
ЕФФцУќЬтЪЧШє![]() ЪЧецУќЬт.
ЪЧецУќЬт.
ЙЪД№АИЮЊЃКD.
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
9
ЁОЬтФПЁПЁАЫЋЧњЯпЕФЗНГЬЮЊ![]() ЁБЪЧЁАЫЋЧњЯпЕФНЅНќЯпЗНГЬЮЊ
ЁБЪЧЁАЫЋЧњЯпЕФНЅНќЯпЗНГЬЮЊ![]() ЁБЕФЃЈ ЃЉ
ЁБЕФЃЈ ЃЉ
A. ГфЗжВЛБивЊЬѕМў B. БивЊВЛГфЗжЬѕМў
C. ГфЗжБивЊЬѕМў D. МШВЛГфЗжвВВЛБивЊЬѕМў
 ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЛГі![]() ЭМЯёЃЌВЂаДГіЕЅЕїЕндіЧјМф(ВЛашвЊЫЕУїРэгЩ)ЃЛ
ЭМЯёЃЌВЂаДГіЕЅЕїЕндіЧјМф(ВЛашвЊЫЕУїРэгЩ)ЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊaЃО0ЧвТњзуВЛЕШЪН22a+1ЃО25aЉ2ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓВЛЕШЪНlogaЃЈ3x+1ЃЉЃМlogaЃЈ7Љ5xЃЉЃЛ
ЃЈ3ЃЉШєКЏЪ§y=logaЃЈ2xЉ1ЃЉдкЧјМф[1ЃЌ3]газюаЁжЕЮЊЉ2ЃЌЧѓЪЕЪ§aЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЪЧRЩЯЕФХМКЏЪ§ЃЌЦфжаeЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЎ
ЪЧRЩЯЕФХМКЏЪ§ЃЌЦфжаeЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЬНОПКЏЪ§![]() дк
дк![]() ЩЯЕФЕЅЕїадЃЌВЂжЄУїФуЕФНсТлЃЛ
ЩЯЕФЕЅЕїадЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉШєКЏЪ§![]() гаСуЕуЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
гаСуЕуЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГМвЭЅНјааРэВЦЭЖзЪЃЌгаСНжжЗНЪНЃЌМзЮЊЭЖзЪеЎШЏЕШЮШНЁаЭВњЦЗЃЌввЮЊЭЖзЪЙЩЦБЕШЗчЯеаЭВњЦЗЃЌЩшЭЖзЪМзЁЂввСНжжВњЦЗЕФФъЪевцЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЭђдЊЃЌИљОнГЄЦкЪевцТЪЪаГЁдЄВтЃЌЫќУЧгыЭЖШызЪН№
ЭђдЊЃЌИљОнГЄЦкЪевцТЪЪаГЁдЄВтЃЌЫќУЧгыЭЖШызЪН№![]() ЭђдЊЕФЙиЯЕЗжБ№ЮЊ
ЭђдЊЕФЙиЯЕЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЃЈЦфжа
ЃЌЃЈЦфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЖМЮЊГЃЪ§ЃЉЃЌКЏЪ§
ЖМЮЊГЃЪ§ЃЉЃЌКЏЪ§![]() ЃЌ
ЃЌ![]() ЖдгІЕФЧњЯп
ЖдгІЕФЧњЯп![]() ,
,![]() ШчЭМЫљЪОЃЎ
ШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓКЏЪ§![]() ЁЂ
ЁЂ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєИУМвЭЅЯжга![]() ЭђдЊзЪН№ЃЌШЋВПгУгкРэВЦЭЖзЪЃЌЮЪЃКШчКЮЗжХфзЪН№ФмЪЙвЛФъЕФЭЖзЪЛёЕУзюДѓЪевцЃЌЦфзюДѓЪевцЪЧЖрЩйЭђдЊЃП
ЭђдЊзЪН№ЃЌШЋВПгУгкРэВЦЭЖзЪЃЌЮЪЃКШчКЮЗжХфзЪН№ФмЪЙвЛФъЕФЭЖзЪЛёЕУзюДѓЪевцЃЌЦфзюДѓЪевцЪЧЖрЩйЭђдЊЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЕФЭМЯёгы
ЕФЭМЯёгы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЌдк
ЃЌдк![]() жсгвВрЕФЕквЛИізюИпЕуКЭЕквЛИігы
жсгвВрЕФЕквЛИізюИпЕуКЭЕквЛИігы![]() жсНЛЕуЗжБ№ЮЊ
жсНЛЕуЗжБ№ЮЊ![]()
ЃЈ1ЃЉЧѓ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНЋКЏЪ§![]() ЭМЯёЩЯЫљгаЕуЕФКсзјБъБфЮЊдРДЕФ
ЭМЯёЩЯЫљгаЕуЕФКсзјБъБфЮЊдРДЕФ![]() БЖЃЈзнзјБъВЛБфЃЉЃЌдйНЋЫљЕУЭМЯёби
БЖЃЈзнзјБъВЛБфЃЉЃЌдйНЋЫљЕУЭМЯёби![]() жсе§ЗНЯђЦНвЦ
жсе§ЗНЯђЦНвЦ![]() ИіЕЅЮЛЃЌЕУЕНКЏЪ§
ИіЕЅЮЛЃЌЕУЕНКЏЪ§![]() ЕФЭМЯёЃЌЧѓ
ЕФЭМЯёЃЌЧѓ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЧѓКЏЪ§![]() дк
дк![]() ЩЯЕФжЕгђЁЃ
ЩЯЕФжЕгђЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉЕФНЙЕуЮЊ
ЃЉЕФНЙЕуЮЊ![]() ЃЌвбжЊЕу
ЃЌвбжЊЕу![]() ЃЌ
ЃЌ ![]() ЮЊХзЮяЯпЩЯЕФСНИіЖЏЕуЃЌЧвТњзу
ЮЊХзЮяЯпЩЯЕФСНИіЖЏЕуЃЌЧвТњзу![]() .Й§Яв
.Й§Яв![]() ЕФжаЕу
ЕФжаЕу![]() зїХзЮяЯпзМЯпЕФДЙЯп
зїХзЮяЯпзМЯпЕФДЙЯп![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФзюДѓжЕЮЊ__________ЃЎ
ЕФзюДѓжЕЮЊ__________ЃЎ
ЁОД№АИЁП1
ЁОНтЮіЁПЩш![]() ЃЌдкШ§НЧаЮABFжаЃЌгУгрЯвЖЈРэЕУЕН
ЃЌдкШ§НЧаЮABFжаЃЌгУгрЯвЖЈРэЕУЕН![]()
![]() ЃЌ
ЃЌ 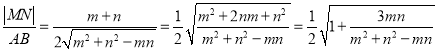
 ЙЪзюДѓжЕЮЊ1.
ЙЪзюДѓжЕЮЊ1.
ЙЪД№АИЮЊЃК1.
ЕуОІЃКБОЬтжївЊПМВщСЫХзЮяЯпЕФМђЕЅаджЪЃЎНтЬтЕФЙиМќЪЧРћгУСЫХзЮяЯпЕФЖЈвхЁЃвЛАуКЭХзЮяЯпгаЙиЕФаЁЬтЃЌКмЖрЪБПЩвдгІгУНсТлРДДІРэЕФЃЛЦНЪБСЗЯАЪБгІЖрзЂвтХзЮяЯпЕФНсТлЕФзмНсКЭгІгУЁЃгШЦфКЭНЙАыОЖСЊЯЕЕФЬтФПЃЌвЛАуЖМКЭЖЈвхгаЙиЃЌЪЕЯжЕуЕуОрКЭЕуЯпОрЕФзЊЛЏЁЃ
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
17
ЁОЬтФПЁПЩш![]() ЕФФкНЧ
ЕФФкНЧ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЫљЖдЕФБпЗжБ№ЮЊ
ЫљЖдЕФБпЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ ![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжмГЄ.
ЕФжмГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDФкНггкЁбOЃЌЙ§ЕуAзїЁбOЕФЧаЯпEPНЛCBЕФбгГЄЯпгкPЃЌЁЯPAB=35ЁуЃЎ 
ЃЈ1ЃЉШєBCЪЧЁбOЕФжБОЖЃЌЧѓЁЯDЕФДѓаЁЃЛ
ЃЈ2ЃЉШєЁЯPAB=35ЁуЃЌЧѓжЄЃК ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖP-ABCDжаЃЌЕзУцABCDЮЊСтаЮЃЌЁЯBAD=60ЁуЃЌQЮЊADЕФжаЕу.
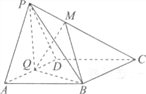
ЃЈЂёЃЉШєPA=PDЃЌЧѓжЄЃКЦНУцPQBЁЭЦНУцPADЃЛ
ЃЈЂђЃЉЕуMдкЯпЖЮPCЩЯЃЌPM=tPCЃЌЪдШЗЖЈЪЕЪ§tЕФжЕЃЌЪЙPAЁЮЦНУцMQBЃЛ
ЃЈЂѓЃЉдкЃЈЂђЃЉЕФЬѕМўЯТЃЌШєЦНУцPADЁЭЦНУцABCDЃЌЧвPA=PD=AD=2ЃЌЧѓЖўУцНЧM-BQ-CЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com