
【题目】如图所示,在直三棱柱![]() ,其中P为棱
,其中P为棱![]() 上的任意一点,设平面PAB与平面
上的任意一点,设平面PAB与平面![]() 的交线为QR.
的交线为QR.

(1)求证:AB∥QR;
(2)若P为棱![]() 上的中点,求几何体
上的中点,求几何体![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)由![]() 可得AB//平面
可得AB//平面![]() ,利用线面平行性质定理可得结果;(2)由题意先明确
,利用线面平行性质定理可得结果;(2)由题意先明确![]() 平面
平面![]() ,利用割补法求体积:几何体QR-ABC的体积为
,利用割补法求体积:几何体QR-ABC的体积为![]() .
.
(1)在直三棱柱![]() 中,
中,
因为![]() ,
,![]() 平面
平面![]() .
.![]() 平面
平面![]() ,
,
所以AB//平面![]() .
.
因为平面PAB与平面![]() 的交线为QR,且
的交线为QR,且![]() 平面PAB,
平面PAB,
所以AB∥QR.
(2)在侧面![]() 中,因为BC=2,
中,因为BC=2,![]() ,P为棱
,P为棱![]() 上的中点,
上的中点,
所以![]() ,
,
所以![]() =∠PBC,所以
=∠PBC,所以![]() ,
,
即![]() .
.
在直三棱柱![]() 中,
中,![]() 平面ABC,
平面ABC,
所以![]() .
.
因为AB=BC=2,AC=![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为BC=2,![]() .
.
所以![]()
又![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 。
。
所以![]() .
.
所以几何体QR-ABC的体积为
![]() ,
,
法二:在侧面![]() 中,因为BC=2,
中,因为BC=2,![]() 为棱
为棱![]() 上的中点,
上的中点,
则![]() .
.
所以有![]() ,
,
所以![]() ,
,
则QR,RP,RC三线相互垂直.
又![]() .
.
在△BPC中,由射影定理,可得![]()
在△ABP中,由三角形相似,可得![]()
则![]() .
.
又![]() .
.
则![]()


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,质量测试分为:指标不小于90为一等品,不小于80小于90为二等品,小于80为三等品,每件一等品盈利50元,每件二等品盈利30元,每件三等品亏损10元,现对学徒工甲和正式工人乙生产的产品各100件的检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 | 5 | 15 | 35 | 35 | 7 | 3 |
乙 | 3 | 7 | 20 | 40 | 20 | 10 |
根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率.
(1)求出乙生产三等品的概率;
(2)求出甲生产一件产品,盈利不小于30元的概率;
(3)若甲、乙一天生产产品分别为40件和30件,估计甲、乙两人一天共为企业创收多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 6 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2020年该地区农村居民家庭人均纯收入约为多少千元?
附:回归直线的斜率和截距的最小二乘估计公式分别为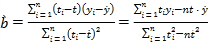 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非
轴的非
负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,求点
两点,求点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AB=AD,BD⊥CD,点E、F分别是棱BC、BD的中点.
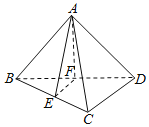
(1)求证:EF∥平面ACD;
(2)求证:AE⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系下,已知圆O:![]() ,直线l:
,直线l:![]() (
(![]() )与圆O相交于A,B两点,且
)与圆O相交于A,B两点,且![]() .
.
(1)求直线l的方程;
(2)若点E,F分别是圆O与x轴的左、右两个交点,点D满足![]() ,点M是圆O上任意一点,点N在线段
,点M是圆O上任意一点,点N在线段![]() 上,且存在常数
上,且存在常数![]() 使得
使得![]() ,求点N到直线l距离的最小值.
,求点N到直线l距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在底面是菱形的四棱锥![]() 中,
中,![]() ,点E在PD上,且
,点E在PD上,且![]() .
.

(1)证明:![]() 平面ABCD;
平面ABCD;
(2)求二面角![]() 的大小;
的大小;
(3)棱PC上是否存在一点F,使![]() 平面AEC?证明你的结论.
平面AEC?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com